Preparata code

In coding theory, the Preparata codes form a class of non-linear double-error-correcting codes. They are named after Franco P. Preparata who first described them in 1968.

Although non-linear over GF(2) the Preparata codes are linear over Z₄ with the Lee distance.

Construction

Let m be an odd number, and 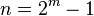$n = 2^m-1$ . We first describe the extended Preparata code of length 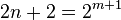$2n+2 = 2^{m+1}$ : the Preparata code is then derived by deleting one position. The words of the extended code are regarded as pairs (X, Y) of 2^m-tuples, each corresponding to subsets of the finite field GF(2^m) in some fixed way.

The extended code contains the words (X, Y) satisfying three conditions

X, Y each have even weight;
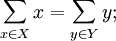
$\sum_{x \in X} x = \sum_{y \in Y} y;$
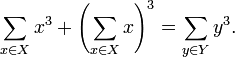
$\sum_{x \in X} x^3 + \left(\sum_{x \in X} x\right)^3 = \sum_{y \in Y} y^3.$

The Peparata code is obtained by deleting the position in X corresponding to 0 in GF(2^m).

Properties

The Preparata code is of length 2^m+1 − 1, size 2^k where k = 2^m + 1 − 2m − 2, and minimum distance 5.

When m = 3, the Preparata code of length 15 is also called the Nordstrom–Robinson code.

References

F.P. Preparata (1968). "A class of optimum nonlinear double-error-correcting codes". Information and Control 13 (4): 378–400. doi:10.1016/S0019-9958(68)90874-7.
J.H. van Lint (1992). Introduction to Coding Theory. GTM 86 (2nd ed.). Springer-Verlag. pp. 111–113. ISBN 3-540-54894-7.
http://www.encyclopediaofmath.org/index.php/Preparata_code
http://www.encyclopediaofmath.org/index.php/Kerdock_and_Preparata_codes