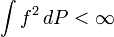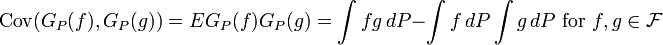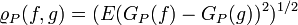Pregaussian class

In probability theory, a pregaussian class or pregaussian set of functions is a set of functions, square integrable with respect to some probability measure, such that there exists a certain Gaussian process, indexed by this set, satisfying the conditions below.

Definition

For a probability space (S, Σ, P), denote by $L^2_P(S)$ a set of square integrable with respect to P functions 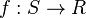$f:S\to R$ , that is

\int f^2 \, dP<\infty

Consider a set 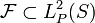$\mathcal{F}\subset L^2_P(S)$ . There exists a Gaussian process 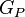$G_P$ , indexed by $\mathcal{F}$ , with mean 0 and covariance

\operatorname{Cov} (G_P(f),G_P(g))= E G_P(f)G_P(g)=\int fg\, dP-\int f\,dP \int g\,dP\text{ for }f,g\in\mathcal{F}

Such a process exists because the given covariance is positive definite. This covariance defines a semi-inner product as well as a pseudometric on 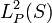$L^2_P(S)$ given by

\varrho_P(f,g)=(E(G_P(f)-G_P(g))^2)^{1/2}

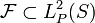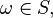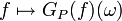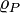Definition A class $\mathcal{F}\subset L^2_P(S)$ is called pregaussian if for each $\omega\in S,$ the function $f\mapsto G_P(f)(\omega)$ on $\mathcal{F}$ is bounded, $\varrho_P$ -uniformly continuous, and prelinear.

Brownian bridge

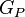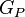The $G_P$ process is a generalization of the brownian bridge. Consider $S=[0,1],$ with P being the uniform measure. In this case, the $G_P$ process indexed by the indicator functions $I_{[0,x]}$ , for $x\in [0,1],$ is in fact the standard brownian bridge B(x). This set of the indicator functions is pregaussian, moreover, it is the Donsker class.

References

R. M. Dudley (1999), Uniform central limit theorems, Cambridge, UK: Cambridge University Press, p. 436, ISBN 0-521-46102-2