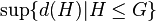Prüfer rank
In mathematics, especially in the area of algebra known as group theory, the Prüfer rank of a pro-p group measures the size of a group in terms of the ranks of its elementary abelian sections.[1] The rank is well behaved and helps to define analytic pro-p-groups. The term is named after Heinz Prüfer.
Definition
The Prüfer rank of pro-p-group  is
is
where 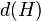 is the rank of the abelian group
is the rank of the abelian group
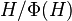 ,
,
where 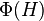 is the Frattini subgroup of
is the Frattini subgroup of  .
.
As the Frattini subgroup of  can be thought of as the group of non-generating elements of
can be thought of as the group of non-generating elements of  , it can be seen that
, it can be seen that 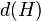 will be equal to the size of any minimal generating set of
will be equal to the size of any minimal generating set of  .
.
Properties
Those profinite groups with finite Prüfer rank are more amenable to analysis.
Specifically in the case of finitely generated pro-p groups, having finite Prüfer rank is equivalent to having an open normal subgroup that is powerful. In turn these are precisely the class of pro-p groups that are p-adic analytic - that is groups that can be imbued with a p-adic manifold structure.
References
- ↑ Yamagishi, Masakazu (2007), "An analogue of the Nielsen-Schreier formula for pro-p-groups", Archiv der Mathematik 88 (4): 304–315, doi:10.1007/s00013-006-1878-4, MR 2311837, Zbl 1119.20035.