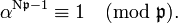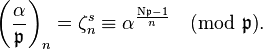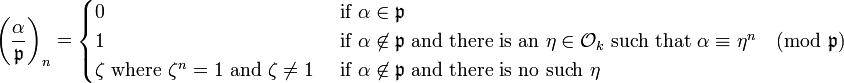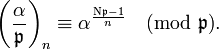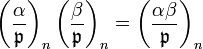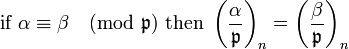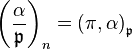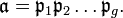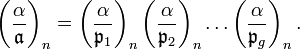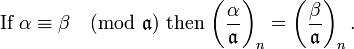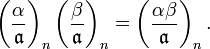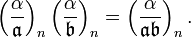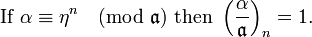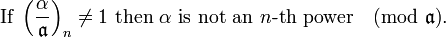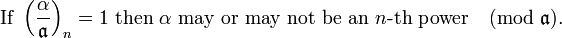Power residue symbol

In algebraic number theory the n-th power residue symbol (for an integer n > 2) is a generalization of the (quadratic) Legendre symbol to n-th powers. These symbols are used in the statement and proof of cubic, quartic, Eisenstein, and related higher^[1] reciprocity laws.^[2]

Background and notation

Let k be an algebraic number field with ring of integers 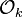$\mathcal{O}_k$ that contains a primitive n-th root of unity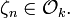 $\zeta_n\in\mathcal{O}_k.$

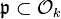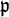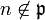Let $\mathfrak{p} \subset \mathcal{O}_k$ be a prime ideal and assume that n and $\mathfrak{p}$ are coprime (i.e. $n \not \in \mathfrak{p}$ .)

The norm of 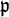$\mathfrak{p}$ is defined as the cardinality of the residue class ring $\mathcal{O}_k / \mathfrak{p}\;:\;\;\; \mathrm{N} \mathfrak{p} = |\mathcal{O}_k / \mathfrak{p}|.$ (since $\mathfrak{p}$ is prime this is a finite field)

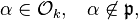There is an analogue of Fermat's theorem in $\mathcal{O}_k:$ If $\alpha \in \mathcal{O}_k,\;\;\; \alpha\not\in \mathfrak{p},$ then

\alpha^{\mathrm{N} \mathfrak{p} -1}\equiv 1 \pmod{\mathfrak{p} }.

And finally, 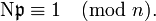$\mathrm{N} \mathfrak{p} \equiv 1 \pmod{n}.$ These facts imply that

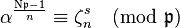\alpha^{\frac{\mathrm{N} \mathfrak{p} -1}{n}}\equiv \zeta_n^s\pmod{\mathfrak{p} }

is well-defined and congruent to a unique n-th root of unity ζ_n^s.

Definition

This root of unity is called the n-th power residue symbol for 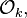$\mathcal{O}_k,$ and is denoted by

\left(\frac{\alpha}{\mathfrak{p} }\right)_n= \zeta_n^s \equiv \alpha^{\frac{\mathrm{N} \mathfrak{p} -1}{n}}\pmod{\mathfrak{p}}.

Properties

The n-th power symbol has properties completely analogous to those of the classical (quadratic) Legendre symbol:

\left(\frac{\alpha}{\mathfrak{p} }\right)_n = \begin{cases} 0 &\mbox{ if } \alpha\in\mathfrak{p}\\ 1 &\mbox{ if }\alpha\not\in\mathfrak{p}\mbox{ and there is an } \eta \in\mathcal{O}_k\mbox{ such that }\alpha\equiv\eta^n\pmod{\mathfrak{p}}\\ \zeta \mbox{ where }\zeta^n=1\mbox{ and }\zeta \neq 1&\mbox{ if }\alpha\not\in\mathfrak{p}\mbox{ and there is no such }\eta \end{cases}

In all cases (zero and nonzero)

\left(\frac{\alpha}{\mathfrak{p} }\right)_n \equiv \alpha^{\frac{\mathrm{N} \mathfrak{p} -1}{n}}\pmod{\mathfrak{p}}.

\left(\frac{\alpha}{\mathfrak{p} }\right)_n \left(\frac{\beta}{\mathfrak{p} }\right)_n = \left(\frac{\alpha\beta}{\mathfrak{p} }\right)_n

\mbox{if }\alpha \equiv\beta\pmod{\mathfrak{p}} \mbox{ then } \left(\frac{\alpha}{\mathfrak{p} }\right)_n = \left(\frac{\beta}{\mathfrak{p} }\right)_n

Relation to the Hilbert symbol

The n-th power residue symbol is related to the Hilbert symbol 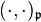$(\cdot,\cdot)_{\mathfrak{p}}$ for the prime 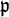$\mathfrak{p}$ by

\left(\frac{\alpha}{\mathfrak{p} }\right)_n = \left({\pi, \alpha}\right)_{\mathfrak{p}}

in the case 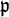$\mathfrak{p}$ coprime to n, where 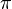$\pi$ is any uniformising element for the local field 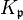$K_{\mathfrak{p}}$ .^[3]

Generalizations

The n-th power symbol may be extended to take non-prime ideals or non-zero elements as its "denominator", in the same way that the Jacobi symbol extends the Legendre symbol.

Any ideal 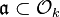$\mathfrak{a}\subset\mathcal{O}_k$ is the product of prime ideals, and in one way only:

\mathfrak{a} = \mathfrak{p}_1 \mathfrak{p}_2 \dots\mathfrak{p}_g.

The n-th power symbol is extended multiplicatively:

\bigg(\frac{\alpha}{\mathfrak{a} }\bigg)_n = \left(\frac{\alpha}{\mathfrak{p}_1 }\right)_n \left(\frac{\alpha}{\mathfrak{p}_2 }\right)_n \dots \left(\frac{\alpha}{\mathfrak{p}_g }\right)_n.

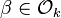If $\beta\in\mathcal{O}_k$ is not zero the symbol 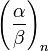$\left(\frac{\alpha}{\beta}\right)_n$ is defined as

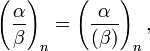\left(\frac{\alpha}{\beta}\right)_n = \left(\frac{\alpha}{(\beta) }\right)_n,

where

(\beta)

is the principal ideal generated by

\beta.

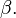
The properties of this symbol are analogous to those of the quadratic Jacobi symbol:

\mbox{If }\alpha\equiv\beta\pmod{\mathfrak{a}} \mbox{ then } \bigg(\frac{\alpha}{\mathfrak{a} }\bigg)_n = \left(\frac{\beta}{\mathfrak{a} }\right)_n.

\bigg(\frac{\alpha}{\mathfrak{a} }\bigg)_n \left(\frac{\beta}{\mathfrak{a} }\right)_n = \left(\frac{\alpha\beta}{\mathfrak{a} }\right)_n.

\left(\frac{\alpha}{\mathfrak{a} }\right)_n \left(\frac{\alpha}{\mathfrak{b} }\right)_n = \left(\frac{\alpha}{\mathfrak{ab} }\right)_n.

\mbox{If } \alpha\equiv\eta^n\pmod{\mathfrak{a}}\mbox{ then } \left(\frac{\alpha}{\mathfrak{a} }\right)_n =1.

\mbox{If } \left(\frac{\alpha}{\mathfrak{a} }\right)_n \neq1 \mbox{ then }\alpha \mbox{ is not an }n\mbox{-th power}\pmod{\mathfrak{a}}.

\mbox{If } \left(\frac{\alpha}{\mathfrak{a} }\right)_n =1 \mbox{ then }\alpha \mbox{ may or may not be an }n\mbox{-th power}\pmod{\mathfrak{a}}.

Power reciprocity law

The power reciprocity law, the analogue of the law of quadratic reciprocity, may be formulated in terms of the Hilbert symbols as^[4]

\left({\frac{\alpha}{\beta}}\right)_n \left({\frac{\beta}{\alpha}}\right)_n^{-1} = \prod_{\mathfrak{p} | n\infty} (\alpha,\beta)_{\mathfrak{p}} \ .

Notes

↑ Quadratic reciprocity deals with squares; higher refers to cubes, fourth, and higher powers.
↑ All the facts in this article are in Lemmermeyer Ch. 4.1 and Ireland & Rosen Ch. 14.2
↑ Neukirch (1999) p. 336
↑ Neukirch (1999) p. 415

References

Gras, Georges (2003), Class field theory. From theory to practice, Springer Monographs in Mathematics, Berlin: Springer-Verlag, pp. 204–207, ISBN 3-540-44133-6, Zbl 1019.11032
Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory (Second edition), New York: Springer Science+Business Media, ISBN 0-387-97329-X

Lemmermeyer, Franz (2000), Reciprocity Laws: from Euler to Eisenstein, Berlin: Springer Science+Business Media, doi:10.1007/978-3-662-12893-0, ISBN 3-540-66957-4, MR 1761696, Zbl 0949.11002
Neukirch, Jürgen (1999), Algebraic number theory, Grundlehren der Mathematischen Wissenschaften 322, Translated from the German by Norbert Schappacher, Berlin: Springer-Verlag, ISBN 3-540-65399-6, Zbl 0956.11021