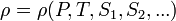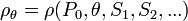Potential density
The potential density of a fluid parcel at pressure  is the density that the parcel would acquire if adiabatically brought to a reference pressure
is the density that the parcel would acquire if adiabatically brought to a reference pressure 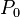 , often 1 bar (100 kPa). Whereas density changes with changing pressure, potential density of a fluid parcel is conserved as the pressure experienced by the parcel changes (provided no mixing with other parcels or net heat flux occurs). The concept is used in oceanography and (to a lesser extent) atmospheric science.
, often 1 bar (100 kPa). Whereas density changes with changing pressure, potential density of a fluid parcel is conserved as the pressure experienced by the parcel changes (provided no mixing with other parcels or net heat flux occurs). The concept is used in oceanography and (to a lesser extent) atmospheric science.
Potential density is a dynamically important property: for static stability potential density must decrease upward. If it doesn't, a fluid parcel displaced upward finds itself lighter than its neighbors, and continues to move upward; similarly, a fluid parcel displaced downward would be heavier than its neighbors. This is true even if the density of the fluid decreases upward. In stable conditions (potential density decreasing upward) motion along surfaces of constant potential density (isopycnals) is energetically favored over flow across these surfaces (diapycnal flow), so most of the motion within a 3-D geophysical fluid takes place along these 2-D surfaces.
In oceanography, the symbol 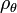 is used to denote potential density, with the reference pressure
is used to denote potential density, with the reference pressure 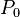 taken to be the pressure at the ocean surface. The corresponding potential density anomaly is denoted by
taken to be the pressure at the ocean surface. The corresponding potential density anomaly is denoted by 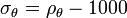 kg/m3. Because the compressibility of seawater varies with salinity and temperature, the reference pressure must chosen to be near the actual pressure to keep the definition of potential density dynamically meaningful. Reference pressures are often chosen as a whole multiple of 100 bar; for water near a pressure of 400 bar (40 MPa), say, the reference pressure 400 bar would be used, and the potential density anomaly symbol would be written
kg/m3. Because the compressibility of seawater varies with salinity and temperature, the reference pressure must chosen to be near the actual pressure to keep the definition of potential density dynamically meaningful. Reference pressures are often chosen as a whole multiple of 100 bar; for water near a pressure of 400 bar (40 MPa), say, the reference pressure 400 bar would be used, and the potential density anomaly symbol would be written 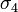 .
Using these reference pressures can be defined the potential density surfaces, used in the analyses of ocean data and to construct models of the ocean current. Neutral density surfaces, defined using another variable called neutral density (
.
Using these reference pressures can be defined the potential density surfaces, used in the analyses of ocean data and to construct models of the ocean current. Neutral density surfaces, defined using another variable called neutral density (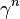 ), can be considered the continuous analog of these potential density surfaces.
), can be considered the continuous analog of these potential density surfaces.
Potential density adjusts for the effect of compression in two ways:
- The effect of a parcel's change in volume due to a change in pressure (as pressure increases, volume decreases).
- The effect of the parcel's change in temperature due to adiabatic change in pressure (as pressure increases, temperature increases).
A parcel's density may be calculated from an equation of state:
where  is temperature,
is temperature,  is pressure and
is pressure and 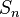 are other tracers that affect density (e.g. salinity of seawater). The potential density would then be calculated as:
are other tracers that affect density (e.g. salinity of seawater). The potential density would then be calculated as:
where  is the potential temperature of the fluid parcel for the same reference pressure
is the potential temperature of the fluid parcel for the same reference pressure 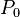 .
.
See also
References
- John M. Wallace and Peter V. Hobbs (2006). Atmospheric Science, An Introductory Survey, Second Edition. Academic Press. ISBN 0-12-732950-1.
- Robert H. Stewart (2002). Introduction to Physical Oceanography.