Post-quantum cryptography

Post-quantum cryptography refers to cryptographic algorithms (usually public-key algorithms) that are thought to be secure against an attack by a quantum computer. This is unlike most currently used public-key algorithms which are efficiently broken by a sufficiently large quantum computer. The concern over current algorithms is that their security relies on the integer factorization problem, the discrete logarithm problem or the elliptic curve discrete logarithm problem. All of these problems can be easily solved on a sufficiently large quantum computer running Shor's algorithm.^[1][2] Even though current, publicly known, experimental quantum computers are too small to attack any real cryptographic algorithm,^[3] many cryptographers are designing new algorithms to prepare for a time when quantum computing becomes a threat. This work has gained greater attention from academics and industry through the PQCrypto conference series since 2006 and more recently by several European Telecommunications Standards Institute (ETSI) Workshops on Quantum Safe Cryptography.^[4][5][6]

In contrast to the threat quantum computing poses to current public key algorithms, most current symmetric cryptographic algorithms (symmetric ciphers and hash functions) are considered to be relatively secure from attacks by quantum computers.^[2][7] While the quantum Grover's algorithm does speed up attacks against symmetric ciphers, moderate increases in key sizes can effectively block these attacks.^[8] Thus post-quantum symmetric cryptography does not need to differ significantly from current symmetric cryptography. See Section on Symmetric Key Approach below.

Post-quantum cryptography is also distinct from quantum cryptography, which refers to using quantum phenomena to achieve secrecy.

Algorithms

Currently post-quantum cryptography research is mostly focused on six different approaches:^[2][5]

Lattice-based Cryptography

This approach includes cryptographic systems such as Ring-Learning with Errors^[9][10][11] or the older NTRU or GGH encryption schemes. According to Micciancio and Regev, Lattice-based Cryptography can be divided into two categories: practical and efficiency oriented schemes like NTRU and the more recent BLISS type signatures which do not possess a proof of security and theoretical schemes like matrix based Learning with Errors schemes that offer strong proofs of security but use keys which are too large for general use.^[12][13] Research since 2008, however, has been able to merge these two categories and create a new class of cryptographic systems based on lattice problems which are both efficient like NTRU and provably secure like standard LWE. These are the Ring-LWE cryptosystems.^[14] While there are many patents on NTRU and the use of Ring-LWE techniques in homomorphic encryption there appear to be no patents on Ring-LWE techniques for key exchange or signature.

Multivariate Cryptography

This includes cryptographic systems such as the Rainbow (Unbalanced Oil and Vinegar) scheme which is based on the difficulty of solving systems of multivariate equations. As noted in the linked Wikipedia article, various attempts to build secure multivariate equation encryption schemes have failed. However, multivariate signature schemes like Rainbow could provide the basis for a quantum secure digital signature.^[15] There is a patent on the Rainbow Signature Scheme.

Hash-based Cryptography

This includes cryptographic systems such as Lamport signatures and the Merkle signature scheme. Hash based digital signatures were invented in the late 1970s by Ralph Merkle and have been studied ever since as an interesting alternative to number theoretic digital signatures like RSA and DSA. Their primary drawback is that for any Hash based public key, there is a limit on the number of signatures that can be signed using the corresponding set of private keys. This fact had reduced interest in these signatures until interest was revived due to the desire for cryptography that was resistant to attack by quantum computers. There appear to be no patents on the Merkle signature scheme and there exist many non-patented hash functions that could be used with these schemes

Code-based Cryptography

This includes cryptographic systems which rely on error-correcting codes, such as the McEliece and Niederreiter encryption algorithms and the related Courtois, Finiasz and Sendrier Signature scheme. The original McEliece signature using random Goppa codes has withstood scrutiny for over 30 years. However many variants of the McEliece Scheme which seek to introduce more structure into the code used in order to reduce the size of the keys have been shown to be insecure.^[16] There appear to be no patents on the McEliece encryption algorithm

Supersingular Elliptic Curve Isogeny Cryptography

This cryptographic system relies on the properties of supersingular elliptic curves to create a Diffie-Hellman replacement with forward secrecy ^[17] This cryptographic system uses the well studied mathematics of supersingular elliptic curves to create a Diffie-Hellman like key exchange that can serve as a straightforward Quantum computing resistant replacement for the Diffie-Hellman and Elliptic curve Diffie–Hellman key exchange methods that are in widespread use today. Because it works much like existing Diffie-Hellman implementations, it offers forward secrecy which is viewed as important both to prevent mass surveillance by governments but also to protect against the compromise of long term keys through failures.^[18] In 2012, researchers Sun, Tian and Wang of the Chinese State Key Lab for Integrated Service Networks and Xidian University, extended the work of De Feo, Jao, and Plut to create quantum secure digital signatures based on supersingular elliptic curve isogenies.^[19] There are no patents covering this cryptographic system.^[20]

Symmetric Key Quantum Resistance

Provided one uses sufficiently large key sizes, the symmetric key cryptographic systems like AES and SNOW 3G are already resistant to attack by a quantum computer.^[21] Further, key management systems and protocols that use symmetric key cryptography instead of public key cryptography like Kerberos and the 3GPP Mobile Network Authentication Structure are also inherently secure against attack by a quantum computer. Given its widespread deployment in the world already, some researchers recommend expanded use of Kerberos-like symmetric key management as an efficient and effective way to get Post Quantum cryptography today.^[22]

Security Reduction

In cryptography research the provable equivalence of the security of a cryptographic algorithm to some known hard mathematical problem is viewed as an important fact in support of using a given cryptographic systems. These proofs are often called "security reductions." In other words the security of a given cryptographic algorithm is reduced to the security of a known hard problem. Researchers are actively looking for security reductions in the prospects for post quantum cryptography. Current results are given here:

Lattice Based Cryptography - Ring-LWE Key Exchange and Signature

In some versions of Ring-LWE there is a security reduction to the Shortest Vector Problem (SVP) in a Lattice is a lower bound on the security. The SVP is known to be NP-hard.^[23] Two specific Ring-LWE systems which have provable security reductions are the Key Exchange and Key Transport Mechanism defined by Peikert ^[9] and Singh^[24] and one variant of Lyubashevsky's Ring-LWE signatures defined in the paper by Guneysu, Lyubashevsky, and Popplemann.^[10]

Lattice-Based Cryptography - NTRU, BLISS

The security of the NTRU encryption scheme and the BLISS^[13] signature is believed to be related to but not provably reducible to the Closest Vector Problem (CVP) in a Lattice. The CVP is known to be NP-hard^[25]

Multivariate Cryptography - Rainbow

The Rainbow Multivariate Equation Signature Scheme is a member of a class of multivariate quadratic equation cryptosystems called "Unbalanced Oil and Vinegar Cryptosystems" (UOV Cryptosystems) Bulygin, Petzoldt and Buchmann have shown a reduction of generic multivariate quadratic UOV systems to the NP-Hard Multivariate Quadratic Equation Solving problem.^[26]

Hash Based Cryptography - Merkle Trees

In 2005, Garcia proved that there was a security reduction of Merkle Hash Tree signatures to the security of the underlying hash function. He showed that if computationally one-way hash functions exist then the Merkle Hash Tree signature is provably secure. Thus if one used a hash function such as SWIFFT with a provable reduction of security to a known hard problem one would have a provable security reduction of the Merkle Tree signature to a known hard problem. Such hash functions exist.^[27]

Code-based Cryptography - McEliece

Strong security reduction to the Syndrome Decoding Problem (SDP).^[28] The SDP is known to be NP-hard^[29]

Supersingular Elliptic Curve Isogeny Cryptography

Security is related to the problem of constructing an isogeny between two supersingular curves with the same number of points. The most recent investigation of the difficulty of this problem is by Delfs and Galbraith.^[30]

Key sizes

One common characteristic of many post-quantum cryptography algorithms is that they require larger key sizes than commonly used "pre-quantum" public key algorithms. There are often tradeoffs to be made in key size, computational efficiency and ciphertext or signature size. It is therefore difficult to compare one scheme against another in only one dimension like key size. However the following paragraphs provide some publicized key sizes for a fixed level of security.

Lattice Based Cryptography - Ring-LWE Key Exchange

For somewhat greater than 128 bits of security, following Peikert's work, Singh presents a set of parameters which have 6956-bit public keys.^[24] The corresponding private key would be roughly 14000 bits.

Lattice-Based Cryptography - NTRU Encryption

For 128 bits of security in NTRU, Hirschhorn, Hoffstein, Howgrave-Graham and Whyte, recommend using a public key represented as a degree 613 polynomial with coefficients 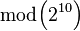. This results in a public key of 6130 bits. The corresponding private key would be 6743 bits.^[31]

Multivariate Cryptography - Rainbow Signature

For 128 bits of security and the smallest signature size in a Rainbow Multivariate Quadratic Equation Signature scheme, Petzoldt, Bulygin and Buchmann, recommend using equations in 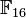with a public key size of just over 1,200,000 bits, a private key of just over 800,000 bits and digital signatrures which are 388 bits in length.^[32]

Hash Based Cryptography - Merkle Trees

In order to get 128 bits of security for hash based signatures to sign 1 million messages using the Fractal Merkle Tree method of Naor Shenhav and Wool the public and private key sizes are roughly 36,000 bits in length.^[33]

Code-based Cryptography - McEliece

For 128 bits of security in a McEliece scheme, Niebuhr, Meziani, Bulygin and Buchmann show that one needs to use a binary Goppa code with a code matrix of at least 2960 x 2288 and capable of correcting 57 errors. With these parameters the public key for the McEliece system will be just under 2,000,000 bits.^[28] According to their work the corresponding private key will be over 12 million bits in length.^[34]

Supersingular Elliptic Curve Isogeny Cryptography

For 128 bits of security in the Supersingular Isogeny Diffie-Hellman (SIDH) method, De Feo, Jao and Plut recommend using a supersingular curve modulo a 768-bit prime. If one uses elliptic curve point compression the public key will need to be no more than 4x768 or 3072 bits in length.^[35] This is the same as the conventional public key sizes that many groups recommend for RSA and Diffie Hellman. Hence the SIDH fits well into existing public key systems.

Symmetric Key Based Cryptography

As a general rule, for 128-bits of security a symmetric key based system one can safely can use key sizes of 256-bits. The best quantum attack against generic symmetric key systems is an application of Grover's algorithm which requires work proportional to the square root of the size of the key space. To transmit an encrypted key to a device which possesses the symmetric key necessary to decrypt that key requires roughly 256 bits as well. It is clear that symmetric key systems offer the smallest key sizes for post quantum cryptography.

The following table is a summary of the information in this section giving the key sizes in bytes:

Algorithm	Public key size (in bytes)	Private key size (in bytes)
Ring-LWE	870	1740
NTRU	767	842
Rainbow	250,000	100,000
Hash signature	4,500	4,500
McEliece	250,000	1,500,000
SIDH	384	384

One practical consideration on a choice for Post Quantum Cryptography concerns how efficiently public keys can be transmitted over the internet. From this point of view, the Ring-LWE, NTRU, and SIDH algorithms seem best suited for general use. Hash signatures come close to being practical from a transmission standpoint. The McEliece and Rainbow schemes seem poorly suited to environments which require transmission of keys.

Forward Secrecy

A public-key system demonstrates a property referred to as perfect forward secrecy when it generates random public keys per session for the purposes of key agreement. This means that the compromise of one message cannot lead to the compromise of others, and also that there is not a single secret value which can lead to the compromise of multiple messages. Security experts recommend using cryptographic algorithms that support forward secrecy over those that do not.^[36] The reason for this is that forward secrecy can protect against the compromise of long term private keys associated with public/private key pairs. This is viewed as a means of preventing mass surveillance by intelligence agencies.

Both the Ring-LWE Key Exchange and Supersingular Isogeny Diffie-Hellman Key Exchange can support forward secrecy in one exchange with the other party. Both the Ring-LWE and SIDH Key Exchange can also be used without forward secrecy by creating a variant of the classic ElGamal encryption variant of Diffie-Hellman

The other algorithms in this article, such as NTRU, do not support forward secrecy in one exchange. These other algorithms could be configured with forward secrecy by generating a new random public key for each key exchange and exchanging random public keys with the other party as a first exchange and then encrypting random numbers with the other party's public key and transmitting the result as a second exchange.

Observations

If one assumes that all of the cryptographic algorithms described above offer at least 128-bits of computational security two key considerations of which algorithm to choose are key size and the ability to provide forward secrecy. The Supersingular Isogeny Diffie-Hellman (SIDH) scheme is the best choice for key size and inherently provides forward secrecy. In some sense it is an optimal replacement for the classic Diffie-Hellman key exchange. The second best replacement for Diffie-Hellman would be the Ring-LWE scheme of Peikert and Ding because of its support for forward secrecy. Unlike SIDH, however, the Ring-LWE construction also has a correspondingly effective digital signature due to Lyubashevski. This could serve as a replacement for Diffie-Hellman (discrete log) based signatures like El Gamal's signature, DSA, ECDSA and the Schnorr signature.

See also

• Quantum computer
• Ideal Lattice Cryptography (Ring-Learning With Errors is one example of Ideal Lattice Cryptography)
• ETSI Quantum Secure Standards Effort
• Topics in Post Quantum Cryptography

References

Further reading

• Post-Quantum Cryptography. Springer. 2008. p. 245. ISBN 978-3540887010. 
• Isogenies in a Quantum World
• On Ideal Lattices and Learning With Errors Over Rings
• Kerberos Revisited: Quantum-Safe Authentication

External links

• PQCrypto, the post-quantum cryptography conference