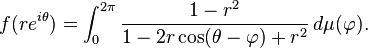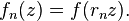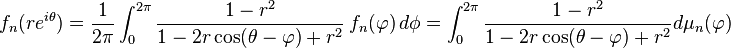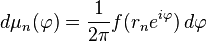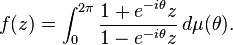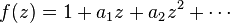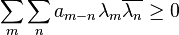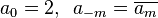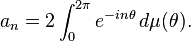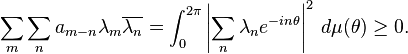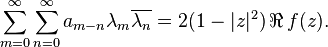Positive harmonic function

In mathematics, a positive harmonic function on the unit disc in the complex numbers is characterized as the Poisson integral of a finite positive measure on the circle. This result, the Herglotz representation theorem, was proved by Gustav Herglotz in 1911. It can be used to give a related formula and characterization for any holomorphic function on the unit disc with positive real part. Such functions had already been characterized in 1907 by Constantin Carathéodory in terms of the positive definiteness of their Taylor coefficients.

Herglotz representation theorem for harmonic functions

A positive function f on the unit disk with f(0) = 1 is harmonic if and only if there is a probability measure μ on the unit circle such that

f(re^{i\theta})=\int_0^{2\pi} {1-r^2\over 1-2r\cos (\theta-\varphi) + r^2} \, d\mu(\varphi).

The formula clearly defines a positive harmonic function with f(0) = 1.

Conversely if f is positive and harmonic and rn increases to 1, define

f_n(z)=f(r_nz). \,

Then

f_n(re^{i\theta}) = {1\over 2\pi}\int_0^{2\pi} {1-r^2\over 1-2r\cos(\theta-\varphi) + r^2 }\, f_n(\varphi)\,d\phi =\int_0^{2\pi}{1-r^2\over 1-2r\cos(\theta-\varphi) + r^2 } d\mu_n(\varphi)

where

d\mu_n(\varphi)={1\over 2\pi} f(r_n e^{i\varphi})\,d\varphi

is a probability measure.

By a compactness argument (or equivalently in this case Helly's selection theorem for Stieltjes integrals), a subsequence of these probability measures has a weak limit which is also a probability measure μ.

Since rn increases to 1, so that fn(z) tends to f(z), the Herglotz formula follows.

Herglotz representation theorem for holomorphic functions

A holomorphic function f on the unit disk with f(0) = 1 has positive real part if and only if there is a probability measure μ on the unit circle such that

f(z) =\int_0^{2\pi} {1 + e^{-i\theta}z\over 1 -e^{-i\theta}z} \, d\mu(\theta).

This follows from the previous theorem because:

Carathéodory's positivity criterion for holomorphic functions

Let

f(z)=1 + a_1 z + a_2 z^2 + \cdots

be a holomorphic function on the unit disk. Then f(z) has positive real part on the disk if and only if

\sum_m\sum_n a_{m-n} \lambda_m\overline{\lambda_n} \ge 0

for any complex numbers λ0, λ1, ..., λN, where

a_0=2,\,\,\, a_{-m} =\overline{a_m}

for m > 0.

In fact from the Herglotz representation for n > 0

a_n =2\int_0^{2\pi} e^{-in\theta}\, d\mu(\theta).

Hence

\sum_m\sum_n a_{m-n} \lambda_m\overline{\lambda_n} =\int_0^{2\pi} \left|\sum_{n} \lambda_n e^{-in\theta}\right|^2 \, d\mu(\theta) \ge 0.

Conversely, setting λn = zn,

\sum_{m=0}^\infty\sum_{n=0}^\infty a_{m-n} \lambda_m\overline{\lambda_n} = 2(1-|z|^2) \,\Re\, f(z).

See also

References