Positive energy theorem
In general relativity, the positive energy theorem (more commonly known as the positive mass conjecture in differential geometry) states that, assuming the dominant energy condition, the mass of an asymptotically flat spacetime is non-negative; furthermore, the mass is zero only for Minkowski spacetime. The theorem is a scalar curvature comparison theorem, with asymptotic boundary conditions, and a corresponding statement of geometric rigidity.
The original proof of the theorem for ADM mass was provided by Richard Schoen and Shing-Tung Yau in 1979 using variational methods. Edward Witten gave another proof in 1981 based on the use of spinors, inspired by positive energy theorems in the context of supergravity. An extension of the theorem for the Bondi mass was given by Ludvigsen and James Vickers, Gary Horowitz and Malcolm Perry, and Schoen and Yau.
Gary Gibbons, Stephen Hawking, Horowitz and Perry proved extensions of the theorem to asymptotically anti-de Sitter spacetimes and to Einstein–Maxwell theory. The mass of an asymptotically anti-de Sitter spacetime is non-negative and only equal to zero for anti-de Sitter spacetime. In Einstein–Maxwell theory, for a spacetime with electric charge 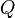 and magnetic charge
and magnetic charge  , the mass of the spacetime satisfies
, the mass of the spacetime satisfies
with equality for the Majumdar–Papapetrou extremal black hole solutions.
See also
- In 1984 Schoen used the positive mass theorem in his work which completed the solution of the Yamabe problem.
- The positive mass theorem was used in Hubert Bray's proof of the Riemannian Penrose inequality.
References
- R. Schoen and S.-T. Yau, "On the proof of the positive mass conjecture in general relativity", Commun. Math. Phys. 65, 45 (1979).
- R. Schoen and S.-T. Yau, "Proof of the positive mass theorem. II", Commun. Math. Phys. 79, 231 (1981).
- E. Witten, "A new proof of the positive energy theorem", Commun. Math. Phys. 80, 381 (1981).
- M. Ludvigsen and J. A. G. Vickers, "The positivity of the Bondi mass", J. Phys. A 14, L389 (1981).
- G. T. Horowitz and M. J. Perry, "Gravitational mass cannot become negative", Phys. Rev. Lett. 48, 371 (1982).
- R. Schoen and S. T. Yau, "Proof that the Bondi mass is positive", Phys. Rev. Lett. 48, 369 (1982).
- G. W. Gibbons, S. W. Hawking, G. T. Horowitz and M. J. Perry, "Positive mass theorems for black holes", Commun. Math. Phys. 88, 295 (1983).