Positional game
Not to be confused with position or positional play in poker.
In the mathematical study of combinatorial games, positional games are games described by a finite set of positions in which a move consists of claiming a previously-unclaimed position. Well-known games that fall into this class include Tic-tac-toe, Hex, and the Shannon switching game.[1] [2]
Definition
A positional game may be described by a pair 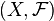 where
where  is a finite set of positions and
is a finite set of positions and  is a family of subsets of
is a family of subsets of  ;
;  is called the board and the sets in
is called the board and the sets in 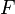 are called winning sets. The game is played by two players who alternately claim unclaimed elements of the board, until all the elements are claimed. The winner may be determined in several ways:
are called winning sets. The game is played by two players who alternately claim unclaimed elements of the board, until all the elements are claimed. The winner may be determined in several ways:
- In a strong positional game, the first player to claim all of the elements of a winning set wins. If the game ends with all elements of the board claimed, but no player has claimed all elements of a winning set, it is a draw. Tic-tac-toe is an example of a strong positional game; in it, the winning sets are all sets of positions that include a subset of three positions in a row.
- In a maker-breaker game, the two players are called Maker and Breaker. Maker wins by claiming all elements of a winning set. If the game ends with all elements of the board claimed, and Maker has not yet won, then Breaker wins. Draws are not possible. In the Shannon switching game, an example of a game of this type, Maker's goal is to claim a set that includes all of the edges in a path between two designated nodes of a graph, and Breaker's goal is to prevent Maker from forming such a path.
- In an avoider-enforcer game, the players are called Avoider and Enforcer. Enforcer wins if Avoider ever claims all of the elements of a winning set. If the game ends with all elements of the board claimed, and Avoider has not claimed a winning set, then Avoider wins. As in maker-breaker games, a draw is not possible.
See also
- Topological game, a generalization of a positional game to infinite sets
- Banach–Mazur game, a game played on a topological space by choosing among certain subsets, with winning conditions resembling those of a maker-breaker game