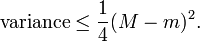Popoviciu's inequality on variances

In probability theory, Popoviciu's inequality, named after Tiberiu Popoviciu, is an upper bound on the variance of any bounded probability distribution. Let M and m be upper and lower bounds on the values of any random variable with a particular probability distribution. Then Popoviciu's inequality states:^[1]

Equality holds precisely when half of the probability is concentrated at each of the two bounds.

Popoviciu's inequality is weaker than the Bhatia–Davis inequality.

References