Polytree
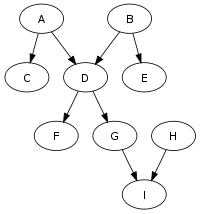
In mathematics, and more specifically in graph theory, a polytree[1] (also known as oriented tree[2][3] or singly connected network[4]) is a directed acyclic graph whose underlying undirected graph is a tree. In other words, if we replace its directed arcs with undirected edges, we obtain an undirected graph that is both connected and acyclic.
A polytree is an example of oriented graph.
The term polytree was coined in 1987 by Rebane and Pearl.[5]
Related structures
Every arborescence (a directed rooted tree, i.e. a directed acyclic graph in which there exists a single source node that has a unique path to every other node) is a polytree, but not every polytree is an arborescence. Every polytree is a multitree, a directed acyclic graph in which the subgraph reachable from any node forms a tree.
The reachability relationship among the nodes of a polytree forms a partial order that has order dimension at most three. If the order dimension is three, there must exist a subset of seven elements x, yi, and zi (for i = 0, 1, 2) such that, for each i, either x ≤ yi ≥ zi, or x ≥ yi ≤ zi, with these six inequalities defining the polytree structure on these seven elements.[6]
A fence or zigzag poset is a special case of a polytree in which the underlying tree is a path and the edges have orientations that alternate along the path. The reachability ordering in a polytree has also been called a generalized fence.[7]
Enumeration
The number of distinct polytrees on n unlabeled nodes, for n = 1, 2, 3, ..., is
Sumner's conjecture
Sumner's conjecture, named after David Sumner, states that tournaments are universal graphs for polytrees, in the sense that every tournament with 2n − 2 vertices contains every polytree with n vertices as a subgraph. Although it remains unsolved, it has been proven for all sufficiently large values of n.[8]
Applications
Polytrees have been used as a graphical model for probabilistic reasoning.[1] If a Bayesian network has the structure of a polytree, then belief propagation may be used to perform inference efficiently on it.[4][5]
The contour tree of a real-valued function on a vector space is a polytree that describes the level sets of the function. The nodes of the contour tree are the level sets that pass through a critical point of the function and the edges describe contiguous sets of level sets without a critical point. The orientation of an edge is determined by the comparison between the function values on the corresponding two level sets.[9]
See also
Notes
- ↑ 1.0 1.1 Dasgupta (1999).
- ↑ Harary & Sumner (1980).
- ↑ Simion (1991).
- ↑ 4.0 4.1 Kim & Pearl (1983).
- ↑ 5.0 5.1 Rebane & Pearl (1987).
- ↑ Trotter & Moore (1977).
- ↑ Ruskey, Frank (1989), "Transposition generation of alternating permutations", Order 6 (3): 227–233, doi:10.1007/BF00563523, MR 1048093
- ↑ Kühn et al. (2011).
- ↑ Carr et al. (2000).
References
- Carr, Hamish; Snoeyink, Jack; Axen, Ulrike (2000), "Computing contour trees in all dimensions", in Proc. 11th ACM-SIAM Symposium on Discrete Algorithms (SODA 2000), pp. 918–926
- Dasgupta, Sanjoy (1999), "Learning polytrees", in Proc. 15th Conference on Uncertainty in Artificial Intelligence (UAI 1999), Stockholm, Sweden, July-August 1999, pp. 134–141.
- Harary, Frank; Sumner, David (1980), "The dichromatic number of an oriented tree", Journal of Combinatorics, Information & System Sciences 5 (3): 184–187, MR 603363.
- Kim, Jin H.; Pearl, Judea (1983), "A computational model for causal and diagnostic reasoning in inference engines", in Proc. 8th International Joint Conference on Artificial Intelligence (IJCAI 1983), Karlsruhe, Germany, August 1983, pp. 190–193.
- Kühn, Daniela; Mycroft, Richard; Osthus, Deryk (2011), "A proof of Sumner's universal tournament conjecture for large tournaments", Proceedings of the London Mathematical Society, Third Series 102 (4): 731–766, arXiv:1010.4430, doi:10.1112/plms/pdq035, MR 2793448.
- Rebane, George; Pearl, Judea (1987), "The recovery of causal poly-trees from statistical data", in Proc. 3rd Annual Conference on Uncertainty in Artificial Intelligence (UAI 1987), Seattle, WA, USA, July 1987, pp. 222–228.
- Simion, Rodica (1991), "Trees with 1-factors and oriented trees", Discrete Mathematics 88 (1): 93–104, doi:10.1016/0012-365X(91)90061-6, MR 1099270.
- Trotter, William T., Jr.; Moore, John I., Jr. (1977), "The dimension of planar posets", Journal of Combinatorial Theory, Series B 22 (1): 54–67, doi:10.1016/0095-8956(77)90048-X.