Polygon-circle graph
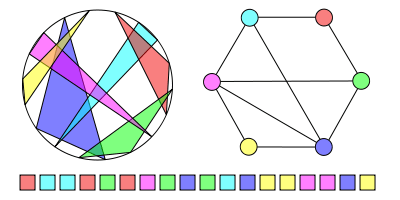
In the mathematical discipline of graph theory, a polygon-circle graph, also called a spider graph, is a type of an intersection graph, where each vertex is represented as a polygon and each edge as an intersection of two polygons representing those vertices, enclosed by a bounding circle. All corners of all polygons lie on the bounding circle. They were first suggested by Michael Fellows in 1988.
A polygon-circle graph can be represented as an "alternating sequence". Such a sequence can be gained by cutting the bounding circle in an arbitrary point and listing the polygons, as we go along. Such sequence is unique.
Recognition
M. Koebe announced a polynomial time recognition algorithm,[1] but it was never published. The algorithm was first published by M. Pergel and J. Kratochvíl.[2]
References
- ↑ M. Koebe. On a new class of intersection graphs in Proceedings of the Fourth Czechoslovak Symposium on Combinatorics Prachatice, pages 141–143, 1990.
- ↑ M. Pergel. Special Graph Classes and Algorithms on Them. Doctoral Thesis, 2007.
- J. P. Spinrad. Efficient Graph Representations. American Mathematical Society, 2003.