Polyadic space
In mathematics, a polyadic space is a topological space that is the image under a continuous function of a topological power of an Alexandroff one-point compactification of a discrete topological space.
History
Polyadic spaces were first studied by S. Mrówka in 1970 as a generalisation of dyadic spaces.[1] The theory was developed further by R. H. Marty, János Gerlits and Murray G. Bell,[2] the latter of whom introduced the concept of the more general centred spaces.[1]
Background
A subset K of a topological space X is said to be compact if every open cover of K contains a finite subcover. It is said to be locally compact at a point x ∈ X if x lies in the interior of some compact subset of X. X is a locally compact space if it is locally compact at every point in the space.[3]
A proper subset A ⊂ X is said to be dense if the closure Ā = X. A space whose set has a countable, dense subset is called a separable space.
For a non-compact, locally compact Hausdorff topological space 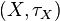 , we define the Alexandroff one-point compactification as the topological space with the set
, we define the Alexandroff one-point compactification as the topological space with the set 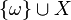 , denoted
, denoted 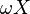 , where
, where 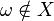 , with the topology
, with the topology 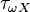 defined as follows:[4][2]
defined as follows:[4][2]
-
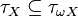
-
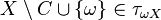 , for every compact subset
, for every compact subset 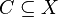 .
.
Definition
Let  be a discrete topological space, and let
be a discrete topological space, and let 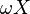 be an Alexandroff one-point compactification of
be an Alexandroff one-point compactification of  . A Hausdorff space
. A Hausdorff space  is polyadic if for some cardinal number
is polyadic if for some cardinal number  , there exists a continuous surjective function
, there exists a continuous surjective function 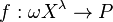 , where
, where 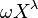 is the product space obtained by multiplying
is the product space obtained by multiplying 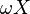 with itself
with itself  times.[5]
times.[5]
Examples
Take the set of natural numbers 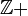 with the discrete topology. Its Alexandroff one-point compactification is
with the discrete topology. Its Alexandroff one-point compactification is 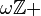 . Choose
. Choose 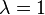 and define the homeomorphism
and define the homeomorphism ![h : \omega \mathbb{Z} + \rightarrow \left [ 0,1 \right ]](../I/m/69ee39640e1cdae9a614843515f670c9.png) with the mapping
with the mapping
It follows from the definition that the space 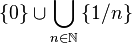 is polyadic and compact directly from the definition of compactness, without using Heine-Borel.
is polyadic and compact directly from the definition of compactness, without using Heine-Borel.
Every dyadic space (a compact space which is a continuous image of a Cantor set[6]) is a polyadic space.[7]
Let X be a separable, compact space. If X is a metrizable space, then it is polyadic (the converse is also true).[2]
Properties
The cellularity 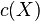 of a space
of a space  is
is 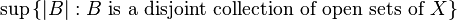 . The tightness
. The tightness 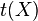 of a space
of a space  is defined as follows: let
is defined as follows: let 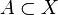 , and
, and 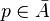 . We define
. We define 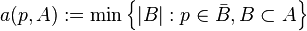 , and define
, and define 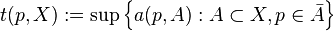 . Then
. Then 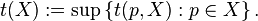 [8] The topological weight
[8] The topological weight 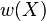 of a polyadic space
of a polyadic space  satisfies the equality
satisfies the equality 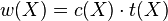 .[9]
.[9]
Let  be a polyadic space, and let
be a polyadic space, and let 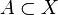 . Then there exists a polyadic space
. Then there exists a polyadic space 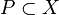 such that
such that 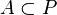 and
and 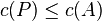 .[9]
.[9]
Polyadic spaces are the smallest class of topological spaces that contain metric compact spaces and are closed under products and continuous images.[10] Every polyadic space  of weight
of weight 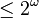 is a continuous image of
is a continuous image of 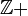 .[10]
.[10]
A topological space X has the Suslin property if there is no uncountable family of pairwise disjoint non-empty open subsets of X.[11] Suppose that X has the Suslin property and X is polyadic. Then X is diadic.[12]
Let 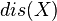 be the least number of discrete sets needed to cover
be the least number of discrete sets needed to cover  , and let
, and let 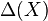 denote the least cardinality of a non-empty open set in
denote the least cardinality of a non-empty open set in  . If
. If  is a polyadic space, then
is a polyadic space, then 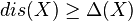 .[9]
.[9]
Ramsey's theorem
There is an analogue of Ramsey's theorem from combinatorics for polyadic spaces. For this, we describe the relationship between Boolean spaces and polyadic spaces. Let 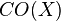 denote the clopen algebra of all clopen subsets of
denote the clopen algebra of all clopen subsets of  . We define a Boolean space as a compact Hausdorff space whose basis is
. We define a Boolean space as a compact Hausdorff space whose basis is 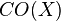 . The element
. The element 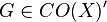 such that
such that 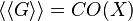 is called the generating set for
is called the generating set for 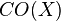 . We say
. We say  is a
is a 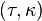 -disjoint collection if
-disjoint collection if  is the union of at most
is the union of at most  subcollections
subcollections 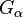 , where for each
, where for each  ,
, 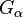 is a disjoint collection of cardinality at most
is a disjoint collection of cardinality at most 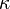 It was proven by Petr Simon that
It was proven by Petr Simon that  is a Boolean space with the generating set
is a Boolean space with the generating set  of
of 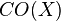 being
being 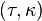 -disjoint if and only if
-disjoint if and only if  is homeomorphic to a closed subspace of
is homeomorphic to a closed subspace of 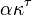 .[8] The Ramsey-like property for polyadic spaces as stated by Murray Bell for Boolean spaces is then as follows: every uncountable clopen collection contains an uncountable subcollection which is either linked or disjoint.[13]
.[8] The Ramsey-like property for polyadic spaces as stated by Murray Bell for Boolean spaces is then as follows: every uncountable clopen collection contains an uncountable subcollection which is either linked or disjoint.[13]
Compactness
We define the compactness number of a space  , denoted by
, denoted by 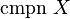 , to be the least number
, to be the least number  such that
such that  has an n-ary closed subbase. We can construct polyadic spaces with arbitrary compactness number. We will demonstrate this using two theorems proven by Murray Bell in 1985. Let
has an n-ary closed subbase. We can construct polyadic spaces with arbitrary compactness number. We will demonstrate this using two theorems proven by Murray Bell in 1985. Let  be a collection of sets and let
be a collection of sets and let  be a set. We denote the set
be a set. We denote the set 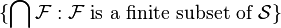 by
by 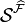 ; all subsets of
; all subsets of  of size
of size  by
by ![[S]^n](../I/m/733b14541cedd680e52b6c151c05216d.png) ; and all subsets of size at most
; and all subsets of size at most  by
by ![[S]^{<=n}](../I/m/371245de85ed8df5664771be043aaf7e.png) . If
. If 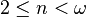 and
and 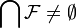 for all
for all ![\mathcal{F} \in [\mathcal{S}]^n](../I/m/c9e3224fa1370d8f2ea1fc4ea6c789f0.png) , then we say that
, then we say that  is n-linked. If every n-linked subset of
is n-linked. If every n-linked subset of  has a non-empty intersection, then we say that
has a non-empty intersection, then we say that  is n-ary. Note that if
is n-ary. Note that if  is n-ary, then so is
is n-ary, then so is 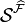 , and therefore every space
, and therefore every space  with
with 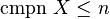 has a closed, n-ary subbase
has a closed, n-ary subbase  with
with 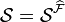 . Note that a collection
. Note that a collection 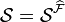 of closed subsets of a compact space
of closed subsets of a compact space  is a closed subbase if and only if for every closed
is a closed subbase if and only if for every closed  in an open set
in an open set  , there exists a finite
, there exists a finite  such that
such that 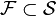 and
and 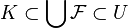 .[14]
.[14]
Let  be an infinite set and let
be an infinite set and let  by a number such that
by a number such that 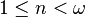 . We define the product topology on
. We define the product topology on ![[S]^{\le n}](../I/m/38fbcfe11a5d36d1d784bd882497709d.png) as follows: for
as follows: for 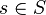 , let
, let ![s^- = \{F \in [S]^{\le n} : s \in F\}](../I/m/e0016579c314dfc00b8c2209ec7bb0ad.png) , and let
, and let ![s^+ = \{F \in [S]^{\le n} : s \notin F\}](../I/m/0c10e8e8ed1bf94276bdb8687b8dba5a.png) . Let
. Let  be the collection
be the collection 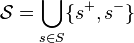 . We take
. We take  as a clopen subbase for our topology on
as a clopen subbase for our topology on ![[S]^{\le n}](../I/m/38fbcfe11a5d36d1d784bd882497709d.png) . This topology is compact and Hausdorff. For
. This topology is compact and Hausdorff. For  and
and  such that
such that 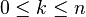 , we have that
, we have that ![[S]^k](../I/m/0445f0863cf0578034b34d944b75e9a5.png) is a discrete subspace of
is a discrete subspace of ![[S]^{\le n}](../I/m/38fbcfe11a5d36d1d784bd882497709d.png) , and hence that
, and hence that ![[S]^{\le n}](../I/m/38fbcfe11a5d36d1d784bd882497709d.png) is a union of
is a union of 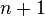 discrete subspaces.[14]
discrete subspaces.[14]
Theorem (Upper bound on ![\operatorname{cmpn}\, [S]^{\le n}](../I/m/5f28d5d38a3f379df83848d95f57a89d.png) ): For each total order
): For each total order 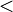 on
on  , there is an
, there is an 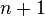 -ary closed subbase
-ary closed subbase 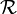 of
of ![[S]^{\le 2n}](../I/m/92c6124177a2356481a20388be207b95.png) .
.
Proof: For 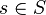 , define
, define 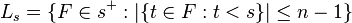 and
and 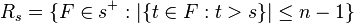 . Set
. Set 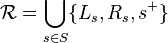 . For
. For  ,
,  and
and  such that
such that 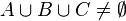 , let
, let 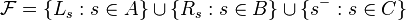 such that
such that  is an
is an 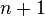 -linked subset of
-linked subset of 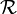 . Show that
. Show that 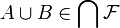 .
. 
For a topological space  and a subspace
and a subspace 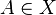 , we say that a continuous function
, we say that a continuous function 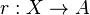 is a retraction if
is a retraction if 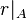 is the identity map on
is the identity map on  . We say that
. We say that  is a retract of
is a retract of  . If there exists an open set
. If there exists an open set  such that
such that 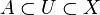 , and
, and  is a retract of
is a retract of  , then we say that
, then we say that  is a neighbourhood retract of
is a neighbourhood retract of  .
.
Theorem (Lower bound on ![\operatorname{cmpn}\, [S]^{\le n}](../I/m/5f28d5d38a3f379df83848d95f57a89d.png) ) Let
) Let  be such that
be such that 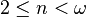 . Then
. Then ![[\omega_1]^{\le 2n-1}](../I/m/b7770d7b20634b193c30c0bb1981a7d9.png) cannot be embedded as a neighbourhood retract in any space
cannot be embedded as a neighbourhood retract in any space  with
with 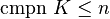 .
.
From the two theorems above, it can be deduced that for  such that
such that 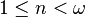 , we have that
, we have that ![\operatorname{cmpn}\,[\omega_1]^{\le 2n-1} = n + 1 = \operatorname{cmpn}\,[\omega_1]^{\le 2n}](../I/m/41a35694e9fa651c2e358322f2e8beb5.png) .
.
Let  be the Alexandroff one-point compactification of the discrete space
be the Alexandroff one-point compactification of the discrete space  , so that
, so that 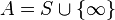 . We define the continuous surjection
. We define the continuous surjection ![g : A^n \rightarrow [S]^{\le n}](../I/m/5600e12a3b72fda8f355f1403e657691.png) by
by 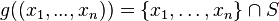 . It follows that
. It follows that ![[S]^{\le n}](../I/m/38fbcfe11a5d36d1d784bd882497709d.png) is a polyadic space. Hence
is a polyadic space. Hence ![[\omega_1]^{\le 2n-1}](../I/m/b7770d7b20634b193c30c0bb1981a7d9.png) is a polyadic space with compactness number
is a polyadic space with compactness number ![\operatorname{cmpn}\, [\omega_1]^{\le 2n-1} = n+1](../I/m/02f6506e0931cb9a3c39a5441953481f.png) .[14]
.[14]
Generalisations
Centred spaces, AD-compact spaces[15] and ξ-adic spaces[16] are generalisations of polyadic spaces.
Centred space
Let  be a collection of sets. We say that
be a collection of sets. We say that  is centred if
is centred if 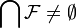 for all finite subsets
for all finite subsets 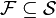 .[17] Define the Boolean space
.[17] Define the Boolean space 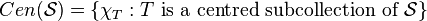 , with the subspace topology from
, with the subspace topology from 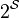 . We say that a space
. We say that a space  is a centred space if there exists a collection
is a centred space if there exists a collection  such that
such that  is a continuous image of
is a continuous image of 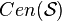 .[18]
.[18]
Centred spaces were introduced by Murray Bell in 2004.
AD-compact space
Let  be a non-empty set, and consider a family of its subsets
be a non-empty set, and consider a family of its subsets 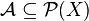 . We say that
. We say that 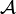 is an adequate family if:
is an adequate family if:
-
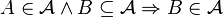
- given
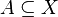 , if every finite subset of
, if every finite subset of  is in
is in 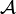 , then
, then 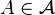 .
.
We may treat 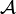 as a topological space by considering it a subset of the Cantor cube
as a topological space by considering it a subset of the Cantor cube 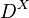 , and in this case, we denote it
, and in this case, we denote it 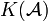 .
.
Let  be a compact space. If there exist a set
be a compact space. If there exist a set  and an adequate family
and an adequate family 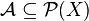 , such that
, such that  is the continuous image of
is the continuous image of 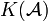 , then we say that
, then we say that  is an AD-compact space.
is an AD-compact space.
AD-compact spaces were introduced by Grzegorz Plebanek. He proved that they are closed under arbitrary products and Alexandroff compactifications of disjoint unions. It follows that every polyadic space is hence an AD-compact space. The converse is not true, as there are AD-compact spaces that are not polyadic.[15]
ξ-adic space
Let 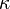 and
and  be cardinals, and let
be cardinals, and let  be a Hausdorff space. If there exists a continuous surjection from
be a Hausdorff space. If there exists a continuous surjection from 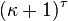 to
to  , then
, then  is said to be a ξ-adic space.[16]
is said to be a ξ-adic space.[16]
ξ-adic spaces were proposed by S. Mrówka, and the following results about them were given by János Gerlits (they also apply to polyadic spaces, as they are a special case of ξ-adic spaces).[19]
Let 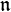 be an infinite cardinal, and let
be an infinite cardinal, and let  be a topological space. We say that
be a topological space. We say that  has the property
has the property 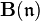 if for any family
if for any family 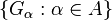 of non-empty open subsets of
of non-empty open subsets of  , where
, where 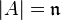 , we can find a set
, we can find a set 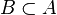 and a point
and a point 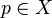 such that
such that 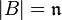 and for each neighbourhood
and for each neighbourhood  of
of  , we have that
, we have that 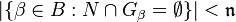 .
.
If  is a ξ-adic space, then
is a ξ-adic space, then  has the property
has the property 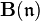 for each infinite cardinal
for each infinite cardinal 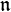 . It follows from this result that no infinite ξ-adic Hausdorff space can be an extremally disconnected space.[19]
. It follows from this result that no infinite ξ-adic Hausdorff space can be an extremally disconnected space.[19]
Hyadic space
Hyadic spaces were introduced by Eric van Douwen.[20] They are defined as follows.
Let  be a Hausdorff space. We denote by
be a Hausdorff space. We denote by 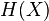 the hyperspace of
the hyperspace of  . We define the subspace
. We define the subspace 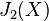 of
of 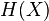 by
by 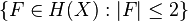 . A base of
. A base of 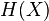 is the family of all sets of the form
is the family of all sets of the form 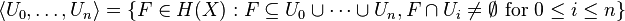 , where
, where  is any integer, and
is any integer, and 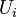 are open in
are open in  . If
. If  is compact, then we say a Hausdorff space
is compact, then we say a Hausdorff space  is hyadic if there exists a continuous surjection from
is hyadic if there exists a continuous surjection from 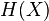 to
to  .[21]
.[21]
Polyadic spaces are hyadic.[22]
See also
References
- ↑ 1.0 1.1 Hart, Klaas Pieter; Nagata, Jun-iti; Vaughan, Jerry E. (2003). "Dyadic compacta". Encyclopedia of General Topology. Elsevier Science. p. 193. ISBN 978-0444503558.
- ↑ 2.0 2.1 2.2 Al-Mahrouqi, Sharifa (2013). Compact topological spaces inspired by combinatorial constructions (Thesis). University of East Anglia. pp. 8–13.
- ↑ Møller, Jesper M. (2014). "Topological spaces and continuous maps". General Topology. p. 58. ISBN 9781502795878.
- ↑ Tkachuk, Vladimir V. (2011). "Basic Notions of Topology and Function Spaces". A Cp-Theory Problem Book: Topological and Function Spaces. Springer Science+Business Media. p. 35. ISBN 9781441974426.
- ↑ Turzański, Marian (1996). Cantor Cubes: Chain Conditions. Wydawnictwo Uniwersytetu Śląskiego. p. 19. ISBN 978-8322607312.
- ↑ Nagata, Jun-Iti. "Topics related to mappings". Modern General Topology. p. 298. ISBN 978-0444876553.
- ↑ Dikranjan, Dikran; Salce, Luigi (1998). Abelian Groups, Module Theory, and Topology. CRC Press. p. 339. ISBN 9780824719371.
- ↑ 8.0 8.1 Bell, Murray (2005). "Tightness in Polyadic Spaces" (PDF). Topology Proceedings (Auburn University) 25: 2–74.
- ↑ 9.0 9.1 9.2 Spadaro, Santi (2009-05-22). "A note on discrete sets". arXiv:abs/0905.3588 Check
|arxiv=value (help). Unsupported parameter(s) in cite arXiv (help) - ↑ 10.0 10.1 Koszmider, Piotr (2012). "Universal Objects and Associations Between Classes of Banach Spaces and Classes of Compact Spaces". arXiv:abs/1209.4294 Check
|arxiv=value (help). Unsupported parameter(s) in cite arXiv (help) - ↑ "Topology Comprehensive Exam" (PDF). Ohio University. 2005. Archived from the original (PDF) on 2014-02-14. Retrieved 2015-02-14.
- ↑ Turzański, Marian (1989). "On generalizations of dyadic spaces". Acta Universitatis Carolinae. Mathematica et Physica 30 (2): 154. ISSN 0001-7140.
- ↑ Bell, Murray (1996-01-11). "A Ramsey Theorem for Polyadic Spaces". University of Tennessee at Martin. Retrieved 2015-02-14.
- ↑ 14.0 14.1 14.2 Bell, Murray (1985). "Polyadic spaces of arbitrary compactness numbers". Commentationes Mathematicae Universitatis Carolinae (Charles University in Prague) 26 (2): 353–361. Retrieved 2015-02-27.
- ↑ 15.0 15.1 Plebanek, Grzegorz (1995-08-25). "Compact spaces that result from adequate families of sets". Topology and its Applications (Elsevier) 65 (3): 257–270.
- ↑ 16.0 16.1 Bell, Murray (1998). "On character and chain conditions in images of products" (PDF). Fundamenta Mathematicae (Polish Academy of Sciences) 158 (1): 41–49.
- ↑ Bell, Murray. "Generalized dyadic spaces" (PDF). pp. 47–58. Archived (PDF) from the original on 2011-06-08. Retrieved 2014-02-27.
- ↑ Bell, Murray (2004). "Function spaces on τ-Corson compacta and tightness of polyadic spaces". Czechoslovak Mathematical Journal 54 (4): 899–914.
- ↑ 19.0 19.1 Gerlits, János (1971). Novák, Josef, ed. "On m-adic spaces". General Topology and its Relations to Modern Analysis and Algebra, Proceedings of the Third Prague Topological Symposium (Prague: Academia Publishing House of the Czechoslovak Academy of Science): 147–148.
- ↑ Bell, Murray (1988). "Gₖ subspaces of hyadic spaces" (PDF). Proceedings of the American Mathematical Society (American Mathematical Society) 104 (2): 635.
- ↑ van Douwen, Eric K. (1990). "Mappings from hyperspaces and convergent sequences". Topology and its Applications (Elsevier) 34 (1): 35–45.
- ↑ Banakh, Taras (2003). "On cardinal invariants and metrizability of topological inverse Clifford semigroups". Topology and its Applications (Elsevier) 128 (1): 38.