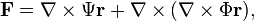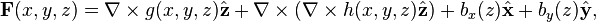Poloidal–toroidal decomposition

In vector analysis, a mathematical discipline, a poloidal–toroidal decomposition of a three-dimensional solenoidal vector field F writes it as a sum of a poloidal vector field and a toroidal vector field:

\mathbf{F} = \nabla \times \Psi \mathbf{r} + \nabla \times (\nabla \times \Phi \mathbf{r}),

Thus, the vector field can be considered to be generated by a pair of scalar potentials Ψ and Φ. This decomposition is a restricted form of Helmholtz decomposition, and has been used in dynamo theory.

Poloidal and toroidal vector fields

A vector field 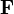\mathbf{F} is called toroidal if it can be written as 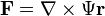\mathbf{F} = \nabla \times \Psi \mathbf{r} for some scalar field 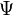\Psi .[1] Every toroidal field is solenoidal, because the divergence of the curl vanishes. A solenoidal vector field 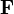\mathbf{F} is toroidal if and only if it is tangential to spheres around the origin ( 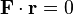\mathbf{F} \cdot \mathbf{r} = 0 ).[2]

A vector field 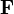\mathbf{F} is called poloidal if it is the curl of a toroidal field; in other words, if there is a scalar field 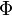\Phi such that 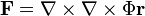\mathbf{F} = \nabla \times \nabla \times \Phi \mathbf{r} .[3] Thus, the curl of a toroidal field is poloidal; reversibly, the curl of a poloidal field is toroidal.[2] This leads to another characterization of poloidal vector fields: a solenoidal vector field is poloidal if and only if its curl is tangential to spheres around the origin.[4]

The decomposition

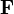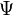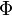Every solenoidal vector field \mathbf{F} can be written as the sum of a toroidal and poloidal field. This decomposition is unique if it is required that the average of the scalar fields \Psi and \Phi vanishes on every sphere of radius r .[3]

Poloidal–toroidal decompositions also exist in Cartesian coordinates, but a mean-field flow has to included in this case. For example, every solenoidal vector field can be written as

\mathbf{F}(x,y,z) = \nabla \times g(x,y,z) \hat{\mathbf{z}} + \nabla \times (\nabla \times h(x,y,z) \hat{\mathbf{z}}) + b_x(z) \hat{\mathbf{x}} + b_y(z)\hat{\mathbf{y}},

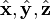where \hat{\mathbf{x}}, \hat{\mathbf{y}}, \hat{\mathbf{z}} denote the unit vectors in the coordinate directions.[5]

See also

Notes

  1. ↑ Backus 1986, p. 87.
  2. ↑ 2.0 2.1 Backus, Parker & Constable 1996, p. 178.
  3. ↑ 3.0 3.1 Backus 1986, p. 88.
  4. ↑ Backus, Parker & Constable 1996, p. 179.
  5. ↑ Jones 2008, p. 62.

References