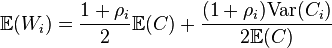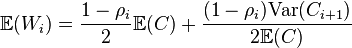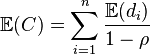Polling system

Polling server serving n queueing nodes

In queueing theory, a discipline within the mathematical theory of probability, a polling system or polling model is a system where a single server visits a set of queues in some order.[1] The model has applications in computer networks and telecommunications,[2] manufacturing[3][4] and road traffic management. The term polling system was coined at least as early as 1968[5][6] and the earliest study of such a system in 1957 where a single repairman servicing machines in the British cotton industry was modelled.[7]

Typically it is assumed that the server visits the different queues in a cyclic manner.[1] Exact results exist for waiting times, marginal queue lengths and joint queue lengths[8] at polling epochs in certain models.[9] Mean value analysis techniques can be applied to compute average quantities.[10]

In a fluid limit, where a very large number of small jobs arrive the individual nodes can be viewed to behave similarly to fluid queues (with a two state process).[11]

Model definition

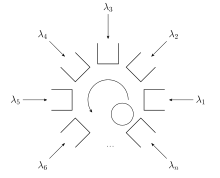
A group of n queues are served by a single server, typically in a cyclic order 1, 2, …, n, 1, …. New jobs arrive at queue i according to a Poisson process of rate λi and are served on a first-come, first-served basis with each job having a service time denoted by a independent and identically distributed random variables Si.

The server chooses when to progress to the next node according to one of the following criteria:[12]

If a queueing node is empty the server immediately moves to serve the next queueing node.

The time taken to switch from serving node i − 1 and node i is denoted by the random variable di.

Utilization

Define ρi = λi E(Si) and write ρ = ρ1 + ρ2 + … + ρn. Then ρ is the long-run fraction of time the server spends attending to customers.[14]

Waiting time

Expected waiting time

For gated service, the expected waiting time at node i is[12]

\mathbb{E}(W_i) = \frac{1+\rho_i}{2} \mathbb{E}(C) + \frac{(1+\rho_i) \text{Var}(C_i)}{2 \mathbb{E}(C)}

and for exhaustive service

\mathbb{E}(W_i) = \frac{1-\rho_i}{2} \mathbb{E}(C) + \frac{(1-\rho_i) \text{Var}(C_{i+1})}{2 \mathbb{E}(C)}

where Ci is a random variable denoting the time between entries to node i and[15]

\mathbb{E}(C) = \sum_{i=1}^n \frac{\mathbb{E}(d_i)}{1-\rho}

The variance of Ci is more complicated and a straightforward calculation requires solving n2 linear equations and n2 unknowns,[16] however it is possible to compute from n equations.[17]

Heavy traffic

The workload process can be approximated by a reflected Brownian motion in a heavily loaded and suitably scaled system if switching servers is immediate[18] and a Bessel process when switching servers takes time.[19]

Applications

Polling systems have been used to model token ring networks.[20]

External links

References

  1. ↑ 1.0 1.1 Boxma, O. J.; Weststrate, J. A. (1989). "Waiting Times in Polling Systems with Markovian Server Routing". Messung, Modellierung und Bewertung von Rechensystemen und Netzen. Informatik-Fachberichte 218. p. 89. doi:10.1007/978-3-642-75079-3_8. ISBN 978-3-540-51713-9.
  2. ↑ Carsten, R.; Newhall, E.; Posner, M. (1977). "A Simplified Analysis of Scan Times in an Asymmetrical Newhall Loop with Exhaustive Service". IEEE Transactions on Communications 25 (9): 951. doi:10.1109/TCOM.1977.1093936.
  3. ↑ Karmarkar, U. S. (1987). "Lot Sizes, Lead Times and In-Process Inventories". Management Science 33 (3): 409–418. doi:10.1287/mnsc.33.3.409. JSTOR 2631860‎.
  4. ↑ Zipkin, P. H. (1986). "Models for Design and Control of Stochastic, Multi-Item Batch Production Systems". Operations Research 34: 91–104. doi:10.1287/opre.34.1.91. JSTOR 170674‎.
  5. ↑ Leibowitz, M. A. (1968). "Queues". Scientific American 219 (2): 96. doi:10.1038/scientificamerican0868-96.
  6. ↑ Takagi, H. (2000). "Analysis and Application of Polling Models". Performance Evaluation: Origins and Directions. LNCS 1769. pp. 423–442. doi:10.1007/3-540-46506-5_18. ISBN 978-3-540-67193-0.
  7. ↑ Mack, C.; Murphy, T.; Webb, N. L. (1957). "The Efficiency of N Machines Uni-Directionally Patrolled by One Operative when Walking Time and Repair Times are Constants". Journal of the Royal Statistical Society. Series B (Methodological) (Wiley for the Royal Statistical Society) 19 (1): 166–172. JSTOR 2984003.
  8. ↑ Resing, J. A. C. (1993). "Polling systems and multitype branching processes". Queueing Systems 13 (4): 409–426. doi:10.1007/BF01149263.
  9. ↑ Borst, S. C. (1995). "Polling systems with multiple coupled servers". Queueing Systems 20 (3–4): 369–393. doi:10.1007/BF01245325.
  10. ↑ Wierman, A.; Winands, E. M. M.; Boxma, O. J. (2007). "Scheduling in polling systems". Performance Evaluation 64 (9–12): 1009. doi:10.1016/j.peva.2007.06.015.
  11. ↑ Czerniak, O.; Yechiali, U. (2009). "Fluid polling systems". Queueing Systems 63: 401. doi:10.1007/s11134-009-9129-6.
  12. ↑ 12.0 12.1 Everitt, D. (1986). "Simple Approximations for Token Rings". IEEE Transactions on Communications 34 (7): 719. doi:10.1109/TCOM.1986.1096599.
  13. ↑ Takagi, H. (1988). "Queuing analysis of polling models". ACM Computing Surveys 20: 5. doi:10.1145/62058.62059.
  14. ↑ Gautam, Natarajan (2012). Analysis of Queues: Methods and Applications. CRC Press. ISBN 9781439806586.
  15. ↑ Eisenberg, M. (1972). "Queues with Periodic Service and Changeover Time". Operations Research 20 (2): 440–451. doi:10.1287/opre.20.2.440. JSTOR 169005‎.
  16. ↑ Ferguson, M. (1986). "Computation of the Variance of the Waiting Time for Token Rings". IEEE Journal on Selected Areas in Communications 4 (6): 775. doi:10.1109/JSAC.1986.1146407.
  17. ↑ Sarkar, D.; Zangwill, W. I. (1989). "Expected Waiting Time for Nonsymmetric Cyclic Queueing Systems—Exact Results and Applications". Management Science 35 (12): 1463. doi:10.1287/mnsc.35.12.1463. JSTOR 2632232.
  18. ↑ Coffman, E. G.; Puhalskii, A. A.; Reiman, M. I. (1995). "Polling Systems with Zero Switchover Times: A Heavy-Traffic Averaging Principle". The Annals of Applied Probability 5 (3): 681. doi:10.1214/aoap/1177004701. JSTOR 2245120.
  19. ↑ Coffman, E. G.; Puhalskii, A. A.; Reiman, M. I. (1998). "Polling Systems in Heavy Traffic: A Bessel Process Limit". Mathematics of Operations Research 23 (2): 257. doi:10.1287/moor.23.2.257. JSTOR 3690512.
  20. ↑ Bux, W. (1989). "Token-ring local-area networks and their performance". Proceedings of the IEEE 77 (2): 238. doi:10.1109/5.18625.