Poisson random measure
Let 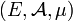 be some measure space with
be some measure space with  -finite measure
-finite measure  . The Poisson random measure with intensity measure
. The Poisson random measure with intensity measure  is a family of random variables
is a family of random variables 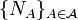 defined on some probability space
defined on some probability space 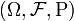 such that
such that
i) 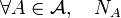 is a Poisson random variable with rate
is a Poisson random variable with rate 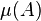 .
.
ii) If sets 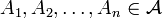 don't intersect then the corresponding random variables from i) are mutually independent.
don't intersect then the corresponding random variables from i) are mutually independent.
iii) 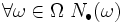 is a measure on
is a measure on 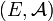
Existence
If 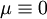 then
then 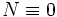 satisfies the conditions i)–iii). Otherwise, in the case of finite measure
satisfies the conditions i)–iii). Otherwise, in the case of finite measure  , given
, given  , a Poisson random variable with rate
, a Poisson random variable with rate 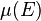 , and
, and  , mutually independent random variables with distribution
, mutually independent random variables with distribution 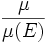 , define
, define 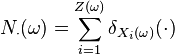 where
where 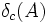 is a degenerate measure located in
is a degenerate measure located in  . Then
. Then  will be a Poisson random measure. In the case
will be a Poisson random measure. In the case  is not finite the measure
is not finite the measure  can be obtained from the measures constructed above on parts of
can be obtained from the measures constructed above on parts of  where
where  is finite.
is finite.
Applications
This kind of random measure is often used when describing jumps of stochastic processes, in particular in Lévy–Itō decomposition of the Lévy processes.
References
- Sato, K. (2010). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press. ISBN 0-521-55302-4.