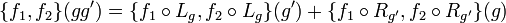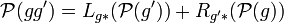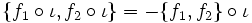Poisson–Lie group

In mathematics, a Poisson–Lie group is a Poisson manifold that is also a Lie group, with the group multiplication being compatible with the Poisson algebra structure on the manifold. The algebra of a Poisson–Lie group is a Lie bialgebra.

Definition

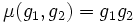A Poisson–Lie group is a Lie group G equipped with a Poisson bracket for which the group multiplication $\mu:G\times G\to G$ with $\mu(g_1, g_2)=g_1g_2$ is a Poisson map, where the manifold G×G has been given the structure of a product Poisson manifold.

Explicitly, the following identity must hold for a Poisson–Lie group:

\{f_1,f_2\} (gg') = \{f_1 \circ L_g, f_2 \circ L_g\} (g') + \{f_1 \circ R_{g^\prime}, f_2 \circ R_{g'}\} (g)

where f₁ and f₂ are real-valued, smooth functions on the Lie group, while g and g' are elements of the Lie group. Here, L_g denotes left-multiplication and R_g denotes right-multiplication.

If 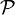$\mathcal{P}$ denotes the corresponding Poisson bivector on G, the condition above can be equivalently stated as

\mathcal{P}(gg') = L_{g \ast}(\mathcal{P}(g')) + R_{g' \ast}(\mathcal{P}(g))

Note that for Poisson-Lie group always 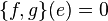$\{f,g\}(e) = 0$ , or equivalently 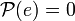$\mathcal{P}(e) = 0$ . This means that non-trivial Poisson-Lie structure is never symplectic, not even of constant rank.

Homomorphisms

A Poisson–Lie group homomorphism 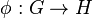$\phi:G\to H$ is defined to be both a Lie group homomorphism and a Poisson map. Although this is the "obvious" definition, neither left translations nor right translations are Poisson maps. Also, the inversion map 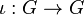$\iota:G\to G$ taking 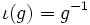$\iota(g)=g^{-1}$ is not a Poisson map either, although it is an anti-Poisson map:

\{f_1 \circ \iota, f_2 \circ \iota \} = -\{f_1, f_2\} \circ \iota

for any two smooth functions 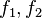$f_1, f_2$ on G.

References

Doebner, H.-D.; Hennig, J.-D., eds. (1989). Quantum groups. Proceedings of the 8th International Workshop on Mathematical Physics, Arnold Sommerfeld Institute, Claausthal, FRG. Berlin: Springer-Verlag. ISBN 3-540-53503-9.
Chari, Vyjayanthi; Pressley, Andrew (1994). A Guide to Quantum Groups. Cambridge: Cambridge University Press. ISBN 0-521-55884-0.