Point-finite collection

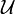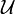In mathematics, a collection $\mathcal{U}$ of subsets of a topological space $X$ is said to be point finite or a point finite collection if every point of $X$ lies in only finitely many members of $\mathcal{U}$ .^[1]

A topological space in which every open cover admits a point-finite open refinement is called metacompact. Every locally finite collection of subsets of a topological space is also point finite. A topological space in which every open cover admits a locally finite open refinement is called paracompact. Every paracompact space is metacompact.^[1]

References

↑ 1.0 1.1 Willard, Stephen (2012), General Topology, Dover Books on Mathematics, Courier Dover Publications, pp. 145–152, ISBN 9780486131788 .

This article incorporates material from point finite on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.