Poincaré separation theorem

In mathematics, the Poincaré separation theorem gives the upper and lower bounds of eigenvalues of a real symmetric matrix B'AB that can be considered as the orthogonal projection of a larger real symmetric matrix A onto a linear subspace spanned by the columns of B. The theorem is named after Henri Poincaré.

More specifically, let A be an n × n real symmetric matrix and B an n × r semi-orthogonal matrix such that B'B = Ir. Denote by 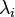\lambda_i, i = 1, 2, ..., n and 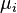\mu_i, i = 1, 2, ..., r the eigenvalues of A and B'AB, respectively (in descending order). We have

\lambda_i \geq \mu_i \geq \lambda_{n-r+i},

Proof

An algebraic proof, based on the variational interpretation of eigenvalues, has been published in Magnus' Matrix Differential Calculus with Applications in Statistics and Econometrics.[1] From the geometric point of view, B'AB can be considered as the orthogonal projection of A onto the linear subspace spanned by B, so the above results follow immediately.[2]

References

  1. ↑ Magnus, Jan R.; Neudecker, Heinz (1988). Matrix Differential Calculus with Applications in Statistics and Econometrics. Hohn Wiley & Sons. p. 209. ISBN 0-471-91516-5.
  2. ↑ Richard Bellman (1 December 1997). Introduction to Matrix Analysis: Second Edition. SIAM. pp. 118–. ISBN 978-0-89871-399-2.

Further reading