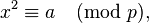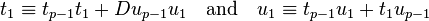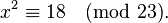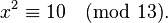Pocklington's algorithm
Pocklington's algorithm is a technique for solving a congruence of the form
where x and a are integers and a is a quadratic residue.
The algorithm is one of the first efficient methods to solve such a congruence. It was described by H.C. Pocklington in 1917.[1]
The algorithm
(Note: all  are taken to mean
are taken to mean  , unless indicated otherwise.)
, unless indicated otherwise.)
Inputs:
- p, an odd prime
- a, an integer which is a quadratic residue
 .
.
Outputs:
- x, an integer satisfying
 . Note that if x is a solution, −x is a solution as well and since p is odd,
. Note that if x is a solution, −x is a solution as well and since p is odd,  . So there is always a second solution when one is found.
. So there is always a second solution when one is found.
Solution method
Pocklington separates 3 different cases for p:
The first case, if 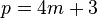 , with
, with 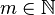 , the solution is
, the solution is 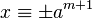 .
.
The second case, if 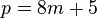 , with
, with 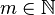 and
and
-
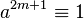 , the solution is
, the solution is 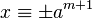 .
. -
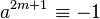 , 2 is a (quadratic) non-residue so
, 2 is a (quadratic) non-residue so 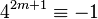 . This means that
. This means that 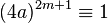 so
so 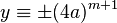 is a solution of
is a solution of  . Hence
. Hence 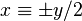 or, if y is odd,
or, if y is odd, 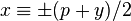 .
.
The third case, if 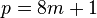 , put
, put 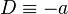 , so the equation to solve becomes
, so the equation to solve becomes 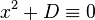 . Now find by trial and error
. Now find by trial and error 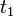 and
and 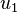 so that
so that 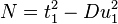 is a quadratic non-residue. Furthermore let
is a quadratic non-residue. Furthermore let
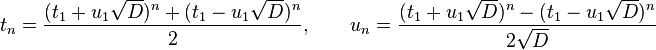 .
.
The following equalities now hold:
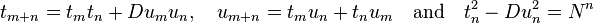 .
.
Supposing that p is of the form 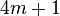 (which is true if p is of the form
(which is true if p is of the form 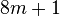 ), D is a quadratic residue and
), D is a quadratic residue and 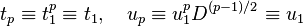 . Now the equations
. Now the equations
give a solution  .
.
Let 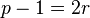 . Then
. Then 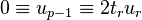 . This means that either
. This means that either 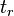 or
or 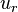 is divisible by p. If it is
is divisible by p. If it is 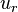 , put
, put 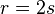 and proceed similarly with
and proceed similarly with 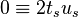 . Not every
. Not every 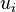 is divisible by p, for
is divisible by p, for 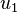 is not. The case
is not. The case 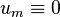 with m odd is impossible, because
with m odd is impossible, because 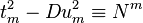 holds and this would mean that
holds and this would mean that 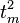 is congruent to a quadratic non-residue, which is a contradiction. So this loop stops when
is congruent to a quadratic non-residue, which is a contradiction. So this loop stops when 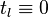 for a particular l. This gives
for a particular l. This gives 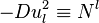 , and because
, and because 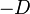 is a quadratic residue, l must be even. Put
is a quadratic residue, l must be even. Put 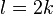 . Then
. Then 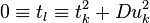 . So the solution of
. So the solution of 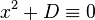 is got by solving the linear congruence
is got by solving the linear congruence 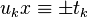 .
.
Examples
The following are 3 examples, corresponding to the 3 different cases in which Pocklington divided forms of p. All  are taken with the modulus in the example.
are taken with the modulus in the example.
Example 1
Solve the congruence
The modulus is 23. This is 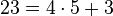 , so
, so 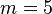 . The solution should be
. The solution should be 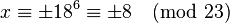 , which is indeed true:
, which is indeed true: 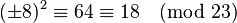 .
.
Example 2
Solve the congruence
The modulus is 13. This is 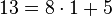 , so
, so 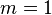 . Now verifying
. Now verifying 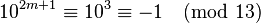 . So the solution is
. So the solution is 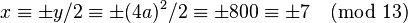 . This is indeed true:
. This is indeed true: 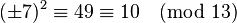 .
.
Example 3
Solve the congruence 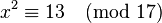 . For this, write
. For this, write 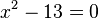 . First find a
. First find a 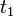 and
and 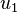 such that
such that 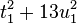 is a quadratic nonresidue. Take for example
is a quadratic nonresidue. Take for example 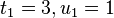 . Now find
. Now find 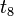 ,
, 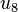 by computing
by computing
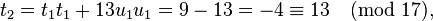 ,
,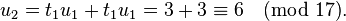
And similarly 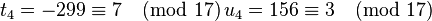 such that
such that 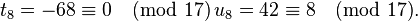
Since 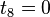 , the equation
, the equation 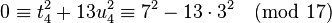 which leads to solving the equation
which leads to solving the equation 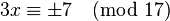 . This has solution
. This has solution 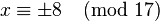 . Indeed,
. Indeed, 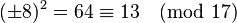 .
.
References
- ↑ H.C. Pocklington, Proceedings of the Cambridge Philosophical Society, Volume 19, pages 57–58
| ||||||||||||||||||||||||||||||||||||||