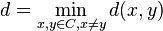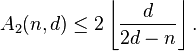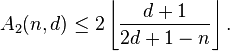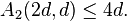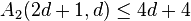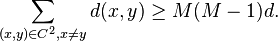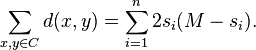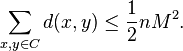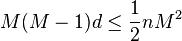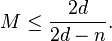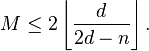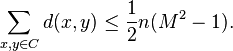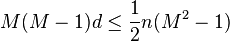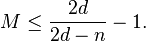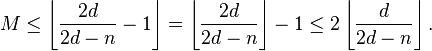Plotkin bound
In the mathematics of coding theory, the Plotkin bound, named after Morris Plotkin, is a limit (or bound) on the maximum possible number of codewords in binary codes of given length n and given minimum distance d.
Statement of the bound
A code is considered "binary" if the codewords use symbols from the binary alphabet 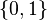 . In particular, if all codewords have a fixed length n,
then the binary code has length n. Equivalently, in this case the codewords can be considered elements of vector space
. In particular, if all codewords have a fixed length n,
then the binary code has length n. Equivalently, in this case the codewords can be considered elements of vector space 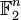 over the finite field
over the finite field 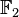 . Let
. Let  be the minimum
distance of
be the minimum
distance of  , i.e.
, i.e.
where 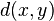 is the Hamming distance between
is the Hamming distance between  and
and  . The expression
. The expression 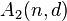 represents the maximum number of possible codewords in a binary code of length
represents the maximum number of possible codewords in a binary code of length  and minimum distance
and minimum distance  . The Plotkin bound places a limit on this expression.
. The Plotkin bound places a limit on this expression.
Theorem (Plotkin bound):
i) If  is even and
is even and 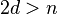 , then
, then
ii) If  is odd and
is odd and 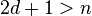 , then
, then
iii) If  is even, then
is even, then
iv) If  is odd, then
is odd, then
where  denotes the floor function.
denotes the floor function.
Proof of case i
Let 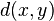 be the Hamming distance of
be the Hamming distance of  and
and  , and
, and  be the number of elements in
be the number of elements in  (thus,
(thus,  is equal to
is equal to 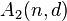 ). The bound is proved by bounding the quantity
). The bound is proved by bounding the quantity 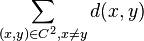 in two different ways.
in two different ways.
On the one hand, there are  choices for
choices for  and for each such choice, there are
and for each such choice, there are 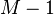 choices for
choices for  . Since by definition
. Since by definition 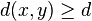 for all
for all  and
and  (
(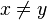 ), it follows that
), it follows that
On the other hand, let  be an
be an 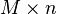 matrix whose rows are the elements of
matrix whose rows are the elements of  . Let
. Let 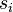 be the number of zeros contained in the
be the number of zeros contained in the  'th column of
'th column of  . This means that the
. This means that the  'th column contains
'th column contains 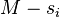 ones. Each choice of a zero and a one in the same column contributes exactly
ones. Each choice of a zero and a one in the same column contributes exactly 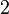 (because
(because 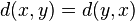 ) to the sum
) to the sum 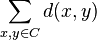 and therefore
and therefore
If  is even, then the quantity on the right is maximized if and only if
is even, then the quantity on the right is maximized if and only if 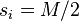 holds for all
holds for all  , then
, then
Combining the upper and lower bounds for 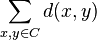 that we have just derived,
that we have just derived,
which given that 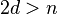 is equivalent to
is equivalent to
Since  is even, it follows that
is even, it follows that
On the other hand, if  is odd, then
is odd, then 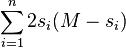 is maximized when
is maximized when 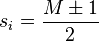 which implies that
which implies that
Combining the upper and lower bounds for 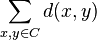 , this means that
, this means that
or, using that 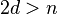 ,
,
Since  is an integer,
is an integer,
This completes the proof of the bound.
See also
- Singleton bound
- Hamming bound
- Elias-Bassalygo bound
- Gilbert-Varshamov bound
- Johnson bound
- Griesmer bound
References
- Plotkin, M. (1960), "Binary codes with specified minimum distance", IRE Transactions on Information Theory 6: 445–450, doi:10.1109/TIT.1960.1057584