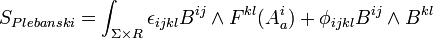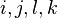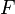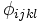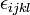Plebanski action
General relativity and supergravity in all dimensions meet each other at a common assumption:
- Any configuration space can be coordinatized by gauge fields
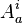 , where the index
, where the index  is a Lie algebra index and
is a Lie algebra index and  is a spatial manifold index.
is a spatial manifold index.
Using these assumptions one can construct an effective field theory in low energies for both. In this form the action of general relativity can be written in the form of the Plebanski action which can be constructed using the Palatini action to derive Einstein's field equations of general relativity.
The form of the action introduced by Plebanski is:
where
are internal indices,
is a curvature on the orthogonal group 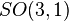 and the connection variables (the gauge fields) are denoted by
and the connection variables (the gauge fields) are denoted by
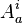 .
.
The symbol
is the Lagrangian multiplier and
is the antisymmetric symbol valued over 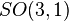 .
.
The specific definition
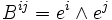 ,
,
which formally satisfies the Einstein's field equation of general relativity.
Application is to the Barrett–Crane model.[1][2]
See also
References
- ↑ Barrett, John W.; Louis Crane (1998), "Relativistic spin networks and quantum gravity", J.Math.Phys. 39: 3296–3302, arXiv:gr-qc/9709028, Bibcode:1998JMP....39.3296B, doi:10.1063/1.532254
- ↑ Barrett, John W.; Louis, Crane, "A Lorentzian signature model for quantum general relativity", Classical and Quantum Gravity 17, arXiv:gr-qc/9904025, Bibcode:2000CQGra..17.3101B, doi:10.1088/0264-9381/17/16/302