Plane wave expansion

In physics, the plane wave expansion expresses a plane wave as a sum of spherical waves,

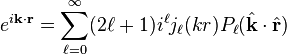e^{i \mathbf k \cdot \mathbf r} = \sum_{\ell = 0}^\infty (2 \ell + 1) i^\ell j_\ell(k r) P_\ell(\hat{\mathbf k} \cdot \hat{\mathbf r})

,

where

$i$ is the imaginary unit,
$k$ is a wave vector of length $k$ ,
$r$ is a position vector of length $r$ ,
$j ℓ$ are spherical Bessel functions,
$P ℓ$ are Legendre polynomials, and
the hat $^$ denotes the unit vector.

In the special case where $k$ is aligned with the z-axis,

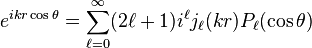e^{i k r \cos \theta} = \sum_{\ell = 0}^\infty (2 \ell + 1) i^\ell j_\ell(k r) P_\ell(\cos \theta)

,

where $θ$ is the spherical polar angle of $r$ .

Expansion in spherical harmonics

With the spherical harmonic addition theorem the equation can be rewritten as

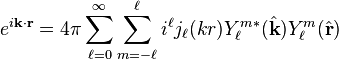e^{i \mathbf{k} \cdot \mathbf{r}} = 4 \pi \sum_{\ell = 0}^\infty \sum_{m = -\ell}^\ell i^\ell j_\ell(k r) Y_\ell^m{}^*(\hat{\mathbf k}) Y_\ell^m(\hat{\mathbf r})

,

where

$Y ℓ m$ are the spherical harmonics and
the superscript $*$ denotes complex conjugation.

Note that the complex conjugation can be interchanged between the two spherical harmonics due to symmetry.

Applications

The plane wave expansion is applied in

Acoustics
Optics
Quantum scattering theory

See also

Helmholtz equation
Plane wave expansion method in computational electromagnetism

References

Digital Library of Mathematical Functions, Equation 10.60.7, National Institute of Standards and Technology
Rami Mehrem, The Plane Wave Expansion, Infinite Integrals and Identities Involving Spherical Bessel Functions