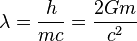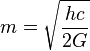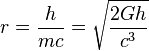Planck particle

A Planck particle, named after physicist Max Planck, is a hypothetical particle defined as a tiny black hole whose Compton wavelength is equal to its Schwarzschild radius.[1] Its mass is thus approximately the Planck mass, and its Compton wavelength and Schwarzschild radius are about the Planck length.[2] Planck particles are sometimes used as an exercise to define the Planck mass and Planck length.[3] They play a role in some models of the evolution of the universe during the Planck epoch.[4]

Compared to a proton, for example, the Planck particle would be extremely small (its radius being equal to the Planck length, which is about 10−20 times the proton's radius) and heavy (the Planck mass being 1019 times the proton's mass).[5]

It is thought that such a particle would vanish in Hawking radiation.

Derivation

While opinions vary as to its proper definition, the most common definition of a Planck particle is a particle whose Compton wavelength is equal to its Schwarzschild radius. This sets the relationship:

\lambda = \frac{h}{m c} = \frac{2 G m}{c^2}

Thus making the mass of such a particle:

m = \sqrt{\frac{h c}{2 G}}

This mass will be 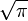\sqrt{\pi } times larger than the Planck mass, making a Planck particle 1.772 times more massive than the Planck unit mass.

Its radius will be the Compton wavelength:

r = \frac{h}{m c} = \sqrt{\frac{2G h}{c^3}}

Dimensions

Using the above derivations we can substitute the universal constants h, G, and c, and determine physical values for the particle's mass and radius. Assuming this radius represents a sphere of uniform density we can further determine the particle's volume and density.

Table 1: Physical dimensions of a Planck particle
Parameter Dimension Value in SI units
Mass M 3.85763×10−8 kg
Radius L 5.72947×10−35 m
Volume L3 7.87827×10−103 m3
Density M L−3 4.89655×1094 kg m−3

It should be noted that the above dimensions do not correspond to any known physical entity or material.

See also

References

  1. ↑ Michel M. Deza; Elena Deza. Encyclopedia of Distances. Springer; 1 June 2009. ISBN 978-3-642-00233-5. p. 433.
  2. ↑ "Light element synthesis in Planck fireballs" - SpringerLink
  3. ↑ B. Roy Frieden; Robert A. Gatenby. Exploratory data analysis using Fisher information. Springer; 2007. ISBN 978-1-84628-506-6. p. 163.
  4. ↑ Harrison, Edward Robert (2000), Cosmology: the science of the universe, Cambridge University Press, ISBN 978-0-521-66148-5 p. 424
  5. ↑ Harrison 2000, p. 478.

External links