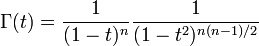Plactic monoid
In mathematics, the plactic monoid is the monoid of all words in the alphabet of positive integers modulo Knuth equivalence. Its elements can be identified with semistandard Young tableaux. It was discovered by Donald Knuth (1970) (who called it the tableau algebra), using an operation given by Craige Schensted (1961) in his study of the longest increasing subsequence of a permutation.
It was named the "monoïde plaxique" by Lascoux & Schützenberger (1981), who allowed any totally ordered alphabet in the definition. The etymology of the word "plaxique" is unclear; it may refer to plate tectonics (tectonique des plaques in French), as the action of a generator of the plactic monoid resembles plates sliding past each other in an earthquake.
Definition
The plactic monoid over some totally ordered alphabet (often the positive integers) is the monoid with the following presentation:
- The generators are the letters of the alphabet
- The relations are the elementary Knuth transformations yzx = yxz whenever x < y ≤ z and xzy = zxy whenever x ≤ y < z.
Knuth equivalence
Two words are called Knuth equivalent if they represent the same element of the plactic monoid, or in other words if one can be obtained from the other by a sequence of elementary Knuth transformations.
Several properties are preserved by Knuth equivalence.
- If a word is a reverse lattice word, then so is any word Knuth equivalent to it.
- If two words are Knuth equivalent, then so are the words obtained by removing their rightmost maximal elements, as are the words obtained by removing their leftmost minimal elements.
- Knuth equivalence preserves the length of the longest nondecreasing subsequence, and more generally preserves the maximum of the sum of the lengths of k disjoint non-decreasing subsequences for any fixed k.
Every word is Knuth equivalent to the word of a unique semistandard Young tableau (this means that each row is non-decreasing and each column is strictly increasing). So the elements of the plactic monoid can be identified with the semistandard Young tableaux, which therefore also form a monoid.
Tableau ring
The tableau ring is the monoid ring of the plactic monoid, so it has a Z-basis consisting of elements of the plactic monoid, with the same product as in the plactic monoid.
There is a homomorphism from the plactic ring on an alphabet to the ring of polynomials (with variables indexed by the alphabet) taking any tableau to the product of the variables of its entries.
Growth
The generating function of the plactic monoid on an alphabet of size n is
showing that there is polynomial growth of dimension 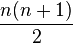 .
.
See also
References
- Duchamp, Gérard; Krob, Daniel (1994), "Plactic-growth-like monoids", Words, languages and combinatorics, II (Kyoto, 1992), World Sci. Publ., River Edge, NJ, pp. 124–142, MR 1351284, Zbl 0875.68720
- Fulton, William (1997), Young tableaux, London Mathematical Society Student Texts 35, Cambridge University Press, ISBN 978-0-521-56144-0, MR 1464693, Zbl 0878.14034
- Knuth, Donald E. (1970), "Permutations, matrices, and generalized Young tableaux", Pacific Journal of Mathematics 34: 709–727, doi:10.2140/pjm.1970.34.709, ISSN 0030-8730, MR 0272654
- Lascoux, Alain; Leclerc, B.; Thibon, J-Y., "The Plactic Monoid", http://www.combinatorics.net/lascoux/articles/plactic.ps Missing or empty
|title=(help) - Littelmann, Peter (1996), "A plactic algebra for semisimple Lie algebras", Advances in Mathematics 124 (2): 312–331, doi:10.1006/aima.1996.0085, ISSN 0001-8708, MR 1424313
- Lascoux, Alain; Schützenberger, Marcel-P. (1981), "Le monoïde plaxique", Noncommutative structures in algebra and geometric combinatorics (Naples, 1978), Quaderni de La Ricerca Scientifica 109, Rome: CNR, pp. 129–156, MR 646486
- Lothaire, M. (2011), Algebraic combinatorics on words, Encyclopedia of Mathematics and Its Applications 90, With preface by Jean Berstel and Dominique Perrin (Reprint of the 2002 hardback ed.), Cambridge University Press, ISBN 978-0-521-18071-9, Zbl 1221.68183
- Schensted, C. (1961), "Longest increasing and decreasing subsequences", Canadian Journal of Mathematics 13 (0): 179–191, doi:10.4153/CJM-1961-015-3, ISSN 0008-414X, MR 0121305
- Schützenberger, Marcel-Paul (1997), "Pour le monoïde plaxique", Mathématiques, Informatique et Sciences Humaines (140): 5–10, ISSN 0995-2314, MR 1627563
Further reading
- Green, James A. (2007), Polynomial representations of GLn, Lecture Notes in Mathematics 830, With an appendix on Schensted correspondence and Littelmann paths by K. Erdmann, J. A. Green and M. Schocker (2nd corrected and augmented ed.), Berlin: Springer-Verlag, ISBN 3-540-46944-3, Zbl 1108.20044