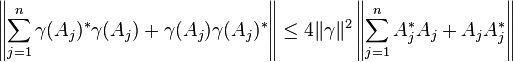Pisier–Ringrose inequality
In mathematics, Pisier–Ringrose inequality is an inequality in the theory of C*-algebras which was proved by Gilles Pisier in 1978 affirming a conjecture of John Ringrose. It is an extension of the Grothendieck inequality.
Statement
Theorem.[1][2] If 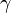 is a bounded, linear mapping of one C*-algebra
is a bounded, linear mapping of one C*-algebra 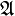 into another C*-algebra
into another C*-algebra 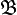 , then
, then
for each finite set 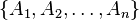 of elements
of elements 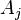 of
of 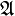 .
.
See Also
- Haagerup-Pisier inequality
- Christensen-Haagerup Principle
Notes
- ↑ Kadison (1993), Theorem D, p. 60.
- ↑ Pisier (1978), Corollary 2.3, p. 410.
References
- Pisier, Gilles (1978), "Grothendieck's theorem for noncommutative C∗-algebras, with an appendix on Grothendieck's constants", Journal of Functional Analysis 29 (3): 397–415, doi:10.1016/0022-1236(78)90038-1, MR 512252.
- Kadison, Richard V. (1993), "On an inequality of Haagerup–Pisier", Journal of Operator Theory 29 (1): 57–67, MR 1277964.