Pierre Fatou

Pierre Fatou
Pierre Fatou
Born 28 February 1878
Lorient
Died 10 August 1929 (aged 51)
Pornichet
Nationality French
Fields Mathematics
Known for Fatou lemma
Fatou set
Fatou–Bieberbach domain

Pierre Joseph Louis Fatou (28 February 1878 – 10 August 1929) was a French mathematician and astronomer. He is known for major contributions to several branches of analysis. The Fatou lemma and the Fatou set are named after him.

Biography

Pierre Fatou

Fatou entered the École Normale Supérieure in Paris in 1898 to study mathematics and graduated in 1901 when he was appointed an observer (stagiaire) in the Paris Observatory. Fatou was promoted to assistant astronomer in 1904 and to astronomer (astronome titulaire) in 1928. He worked in this observatory until his death.

Fatou was awarded the Becquerel prize in 1918; he was a knight of the Legion of Honour (1923).[1] He was the president of the French mathematical society in 1927.[2]

He was in friendly relations with several contemporary French mathematicians, especially, Maurice René Fréchet and Paul Montel.[3]

Mathematical work of Fatou

Fatou's work had very large influence on the development of analysis in the 20th century.

Fatou's PhD thesis Séries trigonométriques et séries de Taylor (Fatou 1906) was the first application of the Lebesgue integral to concrete problems of analysis, mainly to the study of analytic and harmonic functions in the unit disc. In this work, Fatou studied for the first time the Poisson integral of an arbitrary measure on the unit circle. This work of Fatou is influenced by Henri Lebesgue who invented his integral in 1901.

The famous Fatou theorem, which says that a bounded analytic function in the unit disc has radial limits almost everywhere on the unit circle was published in 1906 (Fatou 1906). This theorem was at the origin of a large body of research in 20th-century mathematics under the name of bounded analytic functions.[4] See also the Wikipedia article on functions of bounded type.

A number of fundamental results on the analytic continuation of a Taylor series belong to Fatou.[5]

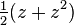Julia set of \tfrac12(z+z^2) investigated by Fatou in 1906. This picture is made with a modern computer.
Julia set of z+1+e−z investigated by Fatou in 1926.
Julia set of a sine function studied by Fatou in 1926

In 1917–1920 Fatou created the area of mathematics which is called holomorphic dynamics (Fatou 1919, 1920, 1920b). It deals with a global study of iteration of analytic functions. He was the first to introduce and study the set which is called now the Julia set. (The complement of this set is sometimes called the Fatou set). Some of the basic results of holomorphic dynamics were also independently obtained by Gaston Julia and Samuel Lattes in 1918. Holomorphic dynamics experienced a strong revival since 1982 because of the new discoveries of Dennis Sullivan, Adrian Douady, John Hubbard and others. Beautiful pictures illustrating this theory produced by modern computers stimulate great interest not only of mathematicians but also outside of the mathematical community. In 1926 Fatou pioneered the study of dynamics of transcendental entire functions, a subject which is intensively developing at this time (2012).

As a byproduct of his studies in holomorphic dynamcis, Fatou discovered what are now called Fatou–Bieberbach domains. These are proper subregions of the complex space of dimension n that are biholomorphically equivalent to the whole space. (Such regions cannot exist for n=1.)

Fatou did important work in celestial mechanics. He was the first to prove rigorously [6] a theorem on the averaging of a perturbation produced by a periodic force of short period, conjectured by Gauss, (Fatou 1928). This work was continued by Leonid Mandelstam and Nikolay Bogolyubov and his students and developed in a large area of modern applied mathematics. Fatou's other research in celestial mechanics includes a study of the movement of a planet in a resisting medium.

Selected publications

See also

Notes

  1. ↑ Audin 2009, p. 138.
  2. ↑ "Anciens Présidents" (in French). French mathematical society.
  3. ↑ Audin 2009, p. 132.
  4. ↑ Garnett, John B. (1981). Bounded analytic functions. Academic Press.
  5. ↑ Bieberbach, Ludwig (1955). Analytische Fortsetzung. Berlin: Springer Verlag.
  6. ↑ Mitropolsky, Iu. A. (1967). "Averaging method in non-linear mechanics". Intl. J. Non-Lin. Mech. 2: 69–95. Bibcode:1967IJNLM...2...69M. doi:10.1016/0020-7462(67)90020-0.

References

External links