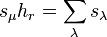Pieri's formula
In mathematics, Pieri's formula, named after Mario Pieri, describes the product of a Schubert cycle by a special Schubert cycle in the Schubert calculus, or the product of a Schur polynomial by a complete symmetric function.
In terms of Schur functions sλ indexed by partitions λ, it states that
where hr is a complete homogeneous symmetric polynomial and the sum is over all partitions λ obtained from μ by adding r elements, no two in the same column.
Pieri's formula implies Giambelli's formula. The Littlewood–Richardson rule is a generalization of Pieri's formula giving the product of any two Schur functions. Monk's formula is an analogue of Pieri's formula for flag manifolds.
References
- Macdonald, I. G. (1995), Symmetric functions and Hall polynomials, Oxford Mathematical Monographs (2nd ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1, MR 1354144
- Sottile, Frank (2001), "S/s130080", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4