Photoacoustic imaging in biomedicine


Photoacoustic imaging, as a hybrid biomedical imaging modality, is developed based on the photoacoustic effect. In photoacoustic imaging, non-ionizing laser pulses are delivered into biological tissues (when radio frequency pulses are used, the technology is referred to as thermoacoustic imaging). Some of the delivered energy will be absorbed and converted into heat, leading to transient thermoelastic expansion and thus wideband (i.e. MHz) ultrasonic emission. The generated ultrasonic waves are detected by ultrasonic transducers and then analyzed to produce images. It is known that optical absorption is closely associated with physiological properties, such as hemoglobin concentration and oxygen saturation.[2] As a result, the magnitude of the ultrasonic emission (i.e. photoacoustic signal), which is proportional to the local energy deposition, reveals physiologically specific optical absorption contrast. 2D or 3D images of the targeted areas can then be formed.[3] Fig. 1 is a schematic illustration showing the basic principles of photoacoustic imaging.

The optical absorption in biological tissues can be due to endogenous molecules such as hemoglobin or melanin, or exogenously delivered contrast agents. As an example, Fig. 2 shows the optical absorption spectra of oxygenated hemoglobin (HbO2) and deoxygenated hemoglobin (Hb) in the visible and near infrared region.[4] Since blood usually has orders of magnitude higher absorption than surrounding tissues, there is sufficient endogenous contrast for photoacoustic imaging to visualize blood vessels. Recent studies have shown that photoacoustic imaging can be used in vivo for tumor angiogenesis monitoring, blood oxygenation mapping, functional brain imaging, skin melanoma detection, etc.[3]
Advantages
| Δf | Primary contrast | Δz | δz | δx | Speed | |
|---|---|---|---|---|---|---|
| Hz | mm | µm | µm | Mvx/s | ||
| Photoacoustic microscopy | 50 M | Optical absorption | 3 | 15 | 45 | 0.5 |
| Photoacoustic tomography | 5 M | Optical absorption | 50 | 700 | 700 | 0.5 |
| Confocal microscopy | Fluorescence, scattering | 0.2 | 3-20 | 0.3-3 | 10-100 | |
| Two-photon microscopy | Fluorescence | 0.5-1.0 | 1-10 | 0.3-3 | 10-100 | |
| Optical coherence tomography | 300 T | Optical scattering | 1-2 | 0.5-10 | 1-10 | 20-4.000 |
| Scanning Laser Acoustic Microscopy | 300 M | Ultrasonic scattering | 1-2 | 20 | 20 | 10 |
| Acoustic microscopy | 50 M | Ultrasonic scattering | 20 | 20-100 | 80-160 | 0.1 |
| Ultrasonography | 5 M | Ultrasonic scattering | 60 | 300 | 300 | 1 |
| Table 1. Comparison of contrast mechanisms, penetration depth (Δz), axial resolution (δz), lateral resolution (δx=δy) and imaging speed of confocal microscopy, two-photon microscopy, optical coherence tomography (300 THz), ultrasound microscopy (50 MHz), ultrasound imaging (5 MHz), photoacoustic microscopy (50 MHz), and photoacoustic tomography (3.5 MHz). Speeds in megavoxel per second of non-parallel techniques. | ||||||
Imaging systems
Two types of photoacoustic imaging systems, photoacoustic/thermoacoustic computed tomography (also known as photoacoustic/thermoacoustic tomography, i.e., PAT/TAT) and photoacoustic microscopy (PAM), have been developed. A typical PAT system uses an unfocused ultrasound detector to acquire the photoacoustic signals, and the image is reconstructed by inversely solving the photoacoustic equations. A PAM system, on the other hand, uses a spherically focused ultrasound detector with 2D point-by-point scanning, and requires no reconstruction algorithm.
Photoacoustic/thermoacoustic/optoacoustic computed tomography (PAT/TAT/OAT)
General equation
Given the heating function 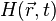 , the generation and propagation of photoacoustic wave pressure
, the generation and propagation of photoacoustic wave pressure 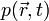 in an acoustically homogeneous inviscid medium is governed by
in an acoustically homogeneous inviscid medium is governed by
where 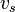 is the speed of sound in medium,
is the speed of sound in medium,  is the thermal expansion coefficient, and
is the thermal expansion coefficient, and 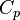 is the specific heat capacity at constant pressure. Eq. (1) holds under thermal confinement to ensure that heat conduction is negligible during the laser pulse excitation. The thermal confinement occurs when the laser pulsewidth is much shorter than the thermal relaxation time.[5]
is the specific heat capacity at constant pressure. Eq. (1) holds under thermal confinement to ensure that heat conduction is negligible during the laser pulse excitation. The thermal confinement occurs when the laser pulsewidth is much shorter than the thermal relaxation time.[5]
The forward solution of Eq. (1) is given by
In stress confinement, which occurs when the laser pulsewidth is much shorter than the stress relaxation time,[5] Eq. (2) can be further derived as
where 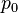 is the initial photoacoustic pressure.
is the initial photoacoustic pressure.
Universal reconstruction algorithm
In a PAT system, the acoustic pressure is detected by scanning an ultrasonic transducer over a surface that encloses the photoacoustic source. To reconstruct the internal source distribution, we need to solve the inverse problem of equation (3) (i.e. to obtain 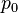 ). A representative method applied for PAT reconstruction is known as the universal backprojection algorithm.[6] This method is suitable for three imaging geometries: planar, spherical, and cylindrical surfaces.
). A representative method applied for PAT reconstruction is known as the universal backprojection algorithm.[6] This method is suitable for three imaging geometries: planar, spherical, and cylindrical surfaces.
The universal backprojection formula is
![\left.p_0(\vec{r})=\int_{\Omega_0} \frac{d \Omega_0}{\Omega_0} \left [2 p(\vec{r_0},v_s t) - 2 v_s t \frac{\partial p(\vec{r_0},v_s t)}{\partial (v_s t)} \right]\right|_{t=|\vec{r} - \vec{r_0}|/v_s},\qquad \quad(4),](../I/m/c63676289ecf30d3a8be4bd1ce57465f.png)
where 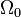 is the solid angle subtended by the entire surface
is the solid angle subtended by the entire surface 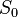 with respect to the reconstruction point
with respect to the reconstruction point 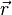 inside
inside 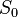 , and
, and
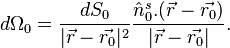
A simple PAT/TAT/OAT system
A simple PAT/TAT/OAT system is shown in the left part of Fig. 3. The laser beam is expanded and diffused to cover the whole region of interest. Photoacoustic waves are generated proportional to the distribution of optical absorption in the target, and are detected by a single scanned ultrasonic transducer. A TAT/OAT system is the same as PAT except that it uses a microwave excitation source instead of a laser. A typical TAT system is shown in the right part of Fig. 3. Although single-element transducers have been employed in these two systems, the detection scheme can be extended to use ultrasound arrays as well.
Biomedical applications of PAT and TAT
Intrinsic optical or microwave absorption contrast and diffraction-limited high spatial resolution of ultrasound make PAT and TAT promising imaging modalities for wide biomedical applications:
Brain lesion detection[9]

Soft tissues with different optical absorption properties in the brain can be clearly identified by PAT. For example, the absorption contrast between the lesion area and the background parenchyma is significant as shown in Fig. 4(a). Fig. 4(b) is the corresponding open-skull photograph after experiment.
Hemodynamics monitoring[7][9]
Since HbO2 and Hb are the dominant absorbing compounds in biological tissues in the visible spectral range, multiple wavelength photoacoustic measurements can be used to reveal the relative concentration of these two chromophores. Thus, the relative total concentration of hemoglobin (HbT) and the hemoglobin oxygen saturation (sO2) can be derived. Therefore, cerebral hemodynamic changes associated with brain function can be successfully detected with PAT.


Fig. 5 is the functional imaging of cerebral hemodynamic changes in response to whisker stimulation. In Fig.5, (a) is the noninvasive PAT image of the vascular pattern in the superficial layer of the rat cortex acquired with the skin and skull intact. (b) and (c) are functional PAT images corresponding to left-side and right-side whisker stimulation, respectively. (d) is the open-skull photograph of the rat cortical surface (B, bregma; L, lambda; M, midline; A, activated regions corresponding to whisker stimulation).
Fig. 6 shows functional changes of sO2 and HbT in the rat cerebral cortex as a result of the physiological modulations. Under the hyperoxia status, the averaged sO2 level, <sO<sub>2>, in the areas of the imaged cortical venous vessels in the rat brain, is higher than that under the normoxia status, and the difference <ΔsO2> is ~10%; while under the hypoxia status, the <sO<sub>2> is lower than that under the normoxia status, and the difference <ΔsO2> is ~13%. While the averaged HbT value, <HbT>, presents a relative increase of ~12%, denoted by <ΔHbT>/<HbT>, as a result of the change from normoxia to hypoxia, which was comparatively larger than the ~4% relative increase in <HbT> as a result of the change from hyperoxia to normoxia.
Breast cancer diagnosis[10]

By utilizing low scattered microwave for excitation, TAT is capable of penetrating thick (several cm) biological tissues with less than mm spatial resolution. Since cancerous tissue and normal tissue have very different responses to radio frequency radiation, TAT has great potential in early breast cancer diagnosis. Fig. 7 shows the TAT image of a mastectomy specimen, where malignant breast tissue generates a much stronger thermoacoustic signal than the surrounding benign tissue due to its high microwave absorption.
Photoacoustic microscopy (PAM)
Fig. 8 shows a representative PAM set-up.[1] A tunable dye laser is pumped by a Q-switched pulsed Nd:YAG (neodymium: yttrium aluminum garnet) laser. A short laser pulse at a certain wavelength between 532-770 nm is generated to irradiate the target tissue to induce acoustic pressure waves. Laser pulses of ~6 mJ/cm2 at the focus will be delivered at 10 Hz repetition rate. An optical fiber of 0.6 mm core diameter is coaxially positioned on a three-dimensional mechanical stage with changeable ultrasonic transducers between 25-75 MHz.
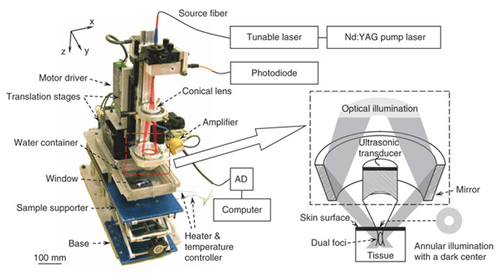

The imaging depth of PAM is mainly limited by the ultrasonic attenuation. The spatial (i.e. axial and lateral) resolutions depend on the ultrasonic transducer used. An ultrasonic transducer with high central frequency and broader bandwidth are chosen to obtain high axial resolution. The lateral resolution is determined by the focal diameter of the transducer. For instance, a 50 MHz ultrasonic transducer provides 15 micrometre axial and 45 micrometre lateral resolution with ~3 mm imaging depth.
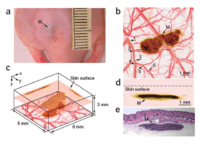
PAM has multiple important applications in functional imaging. Two examples are shown in Figs. 9 and 10. PAM can detect changes in oxygenated/deoxygenated hemoglobin in small vessels. As shown in Fig. 9, arterioles (red) and venules (blue) are clearly delineated with high spatial resolution.[11] Fig. 10 shows the capability of PAM to image skin melanoma by using dual wavelength to obtain the morphological relationship between the melanoma and its surrounding blood vessels structures in vivo.[1]
See also
- Photoacoustic tomography
- Multispectral optoacoustic tomography
- L. V. Wang, "Photoacoustic tomography," Scholarpedia, 9(2):10278(2014).
- L. V. Wang, "Hot Topics presentation: Photoacoustic Tomography -- Ultrasonically Beating Optical Diffusion and Diffraction," SPIE Newsroom, DOI:10.1117/2.3201403.15
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Zhang, H. F. et al. (2006). "Functional photoacoustic microscopy for high-resolution and noninvasive in vivo imaging". Nature Biotechnology 24 (7): 848–851. doi:10.1038/nbt1220. PMID 16823374.
- ↑ A. Grinvald et al. (1986). "Functional architecture of cortex revealed by optical imaging of intrinsic signals". Nature 324 (6095): 361–364. doi:10.1038/324361a0. PMID 3785405.
- ↑ 3.0 3.1 M. Xu and L.H. Wang (2006). "Photoacoustic imaging in biomedicine". Review of Scientific Instruments 77 (4): 041101. doi:10.1063/1.2195024.
- ↑ Optical Properties Spectra
- ↑ 5.0 5.1 L.H. Wang and H.I. Wu (2007). Biomedical Optics. Wiley. ISBN 978-0-471-74304-0.
- ↑ M. Xu et al. (2005). "Universal back-projection algorithm for photoacoustic-computed tomography". Physical Review E 71 (1): 016706. doi:10.1103/PhysRevE.71.016706.
- ↑ 7.0 7.1 7.2 X. Wang et al. (2006). "Non-invasive imaging of hemoglobin concentration and oxygenation in the rat brain using high-resolution photoacoustic tomography". Journal of Biomedical Optics 11 (2): 024015. doi:10.1117/1.2192804. PMID 16674205.
- ↑ X. Jin et al. (2006). "Thermoacoustic tomography with correction for acoustic speed variations". Physics in Medicine and Biology 51 (24): 6437–6448. doi:10.1088/0031-9155/51/24/010. PMID 17148827.
- ↑ 9.0 9.1 9.2 9.3 X. Wang et al. (2003). "Non-invasive laser-induced photoacoustic tomography for structural and functional imaging of the brain in vivo". Nature Biotechnology 21 (7): 803–806. doi:10.1038/nbt839. PMID 12808463.
- ↑ 10.0 10.1 G. Ku et al. (2005). "Thermoacoustic and photoacoustic tomography of thick biological tissues toward breast imaging". Technology in Cancer Research and Treatment 4 (5): 559–566. PMID 16173826.
- ↑ 11.0 11.1 Zhang, H. F. et al. (2007). "Imaging of hemoglobin oxygen saturation variations in single vessels in vivo using photoacoustic microscopy". Applied Physics Letters 90 (5): 053901. doi:10.1063/1.2435697.
External links
- Optical Imaging Laboratory, Department of Biomedical Engineering, Washington University in St. Louis
- Photoacoustic Imaging Group, Department of Medical Physics and Bioengineering, University College London
- Optoacoustic Imaging Lab, Department of Biomedical Photonics, Institute of Applied Physics, University of Bern
- Biomedical Photonic Imaging Group, BioPhysical Engineering Group, Faculty of Science and Technology, University of Twente, Enschede, The Netherlands
- Functional Optical Imaging Laboratory (FOIL), Department of Biomedical Engineering, Northwestern University
- Biophotonics and Imaging Laboratory (BAIL), Department of Biomedical Engineering, Oregon Health & Science University
- OptoSonics, Inc.
- Tomowave Laboratories, Inc.
- Biomedical Optical Imaging Laboratory, Department of Electrical & Computer Engineering, University of Connecticut
- An interdisciplinary consortium of experts in photoacoustic imaging in Austria where research in physics and mathematics is heavily driven by input from biology and medicine
- Recent advances in application of acoustic, acousto-optic and photoacoustic methods in biology and medicine
- Ultrasound Imaging and Therapeutics Research Laboratory, Department of Biomedical Engineering, University of Texas at Austin
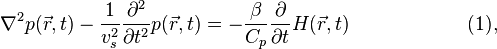
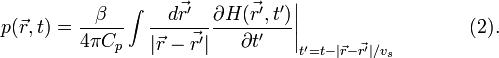
![p(\vec{r},t)=\frac{1}{4 \pi v_s^2} \frac{\partial}{\partial t} \left [\frac{1}{v_s t} \int d \vec{r'} p_0(\vec{r'}) \delta \left (t-\frac{|\vec{r}-\vec{r'}|}{v_s} \right) \right] \qquad \,(3),](../I/m/4375ea56f55508e36b30cb4e804881e6.png)
