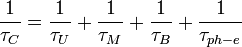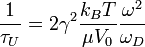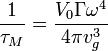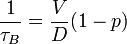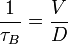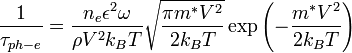Phonon scattering

Phonons can scatter through several mechanisms as they travel through the material. These scattering mechanisms are: Umklapp phonon-phonon scattering, phonon-impurity scattering, phonon-electron scattering, and phonon-boundary scattering. Each scattering mechanism can be characterised by a relaxation rate 1/ $\tau$ which is the inverse of the corresponding relaxation time.

All scattering processes can be taken into account using Matthiessen's rule. Then the combined relaxation time 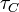$\tau_{C}$ can be written as:

\frac{1}{\tau_C} = \frac{1}{\tau_U}+\frac{1}{\tau_M}+\frac{1}{\tau_B}+\frac{1}{\tau_{ph-e}}

The parameters 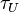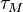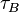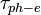$\tau_{U}$ , $\tau_{M}$ , $\tau_{B}$ , $\tau_{ph-e}$ are due to Umklapp scattering, mass-difference impurity scattering, boundary scattering and phonon-electron scattering, respectively.

Phonon-phonon scattering

For phonon-phonon scattering, effects by normal processes (processes which conserve the phonon wave vector - N processes) are ignored in favor of Umklapp processes (U processes). Since normal processes vary linearly with 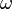$\omega$ and umklapp processes vary with 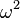$\omega^2$ , Umklapp scattering dominates at high frequency.^[1] 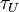$\tau_U$ is given by:

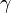\frac{1}{\tau_U}=2\gamma^2\frac{k_B T}{\mu V_0}\frac{\omega^2}{\omega_D}

where $\gamma$ is Gruneisen anharmonicity parameter, μ is shear modulus, V₀ is volume per atom and 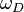$\omega_{D}$ is Debye frequency.^[2]

Mass-difference impurity scattering

Mass-difference impurity scattering is given by:

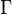\frac{1}{\tau_M}=\frac{V_0 \Gamma \omega^4}{4\pi v_g^3}

where $\Gamma$ is a measure of the impurity scattering strength. Note that 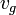${v_g}$ is dependent of the dispersion curves.

Boundary scattering

Boundary scattering is particularly important for low-dimensional nanostructures and its relaxation time is given by:

\frac{1}{\tau_B}=\frac{V}{D}(1-p)

where D is the dimension of the system and p represents the surface roughness parameter. The value p=1 means a smooth perfect surface that the scattering is purely specular and the relaxation time goes to ∞; hence, boundary scattering does not affect thermal transport. The value p=0 represents a very rough surface that the scattering is then purely diffusive which gives:

\frac{1}{\tau_B}=\frac{V}{D}

This equation is also known as Casimir limit.^[3]

Phonon-electron scattering

Phonon-electron scattering can also contribute when the material is lightly doped. The corresponding relaxation time is given as:

\frac{1}{\tau_{ph-e}}=\frac{n_e \epsilon^2 \omega}{\rho V^2 k_B T}\sqrt{\frac{\pi m^* V^2}{2k_B T}} \exp \left(-\frac{m^*V^2}{2k_B T}\right)

The parameter 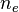$n_{e}$ is conduction electrons concentration, ε is deformation potential, ρ is mass density and m* is effective electron mass.^[2] It is usually assumed that contribution to thermal conductivity by phonon-electron scattering is negligible.

References

↑ Mingo, N (2003). "Calculation of nanowire thermal conductivity using complete phonon dispersion relations". Journal reference: Phys. Rev. B Phys Rev B 68: 113308. arXiv:cond-mat/0308587. Bibcode:2003PhRvB..68k3308M. doi:10.1103/PhysRevB.68.113308.
↑ 2.0 2.1 Zou, Jie; Balandin, Alexander (2001). "Phonon heat conduction in a semiconductor nanowire". Journal of Applied Physics 89 (5): 2932. Bibcode:2001JAP....89.2932Z. doi:10.1063/1.1345515.
↑ Casimir, H.B.G (1938). "Note on the Conduction of Heat in Crystals". Physica, 5 6 (6): 495. Bibcode:1938Phy.....5..495C. doi:10.1016/S0031-8914(38)80162-2.