Phase-shift oscillator

A phase-shift oscillator is a linear electronic oscillator circuit that produces a sine wave output. It consists of an inverting amplifier element such as a transistor or op amp with its output fed back to its input through a phase-shift network consisting of resistors and capacitors. The feedback network 'shifts' the phase of the amplifier output by 180 degrees at the oscillation frequency to give positive feedback.[1] Phase-shift oscillators are often used at audio frequency as audio oscillators.

The filter produces a phase shift that increases with frequency. It must have a maximum phase shift of more than 180 degrees at high frequencies so the phase shift at the desired oscillation frequency can be 180 degrees. The most common phase-shift network cascades three identical resistor-capacitor stages that produce a phase shift of zero at low frequencies and 270° at high frequencies.

Implementation

Op-amp implementation

One of the simplest implementations for this type of oscillator uses an operational amplifier (op-amp), three capacitors and four resistors, as shown in the diagram.

The mathematics for calculating oscillation frequency and oscillation criterion for this circuit are surprisingly complex, due to each RC stage loading the previous ones. The calculations are greatly simplified by setting all the resistors (except the negative feedback resistor) and all the capacitors to the same values. In the diagram, if R1=R2=R3=R, and C1=C2=C3=C, then:

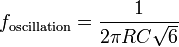
f_\mathrm{oscillation}=\frac{1}{2\pi RC\sqrt{6}}

and the oscillation criterion is:

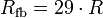
R_\mathrm{fb}=29 \cdot R


Without the simplification of all the resistors and capacitors having the same values, the calculations become more complex:

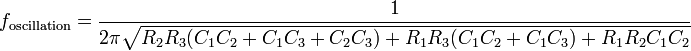
f_\mathrm{oscillation}=\frac{1}{2\pi\sqrt{R_2R_3(C_1C_2+C_1C_3+C_2C_3)+R_1R_3(C_1C_2+C_1C_3)+R_1R_2C_1C_2}}

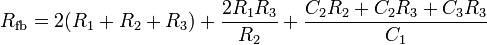
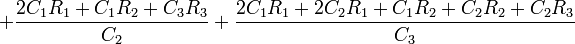
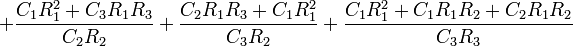
Oscillation criterion: R_\mathrm{fb}= 2(R_1+R_2+R_3) + \frac{2R_1R_3}{R_2} + \frac{C_2R_2+C_2R_3+C_3R_3}{C_1} + \frac{2C_1R_1+C_1R_2+C_3R_3}{C_2} + \frac{2C_1R_1+2C_2R_1+C_1R_2+C_2R_2+C_2R_3}{C_3} + \frac{C_1R_1^2+C_3R_1R_3}{C_2R_2} + \frac{C_2R_1R_3+C_1R_1^2}{C_3R_2} + \frac{C_1R_1^2+C_1R_1R_2+C_2R_1R_2}{C_3R_3}

As with other feedback oscillators, when the power is applied to the circuit, thermal electrical noise in the circuit or the turn-on transient provides an initial signal to start oscillations. The oscillations grow rapidly in amplitude until saturation of the op-amp or transistor limits the gain, and they stabilize at a constant amplitude at which the loop gain of the circuit is unity.

One potential problem with the single op-amp circuit is the high gain required to maintain the oscillation. If it is assumed that each RC segment does not affect the other, a gain of about 8 to 10 will be sufficient to enable oscillation. As mentioned previously, each RC section loads the next section, and a larger gain (about 27 to 30) is required to keep the circuit in oscillation.[2] An improved version of this circuit can be made by putting an op-amp buffer between each RC stage. (This also simplifies the calculations.) Тhe voltage gain of the inverting channel is always unity.

When the oscillation frequency is high enough to be near the amplifier's cutoff frequency, the amplifier will contribute significant phase shift itself, which will add to the phase shift of the feedback network. Therefore the circuit will oscillate at a frequency at which the phase shift of the feedback filter is less than 180 degrees.

FET implementation

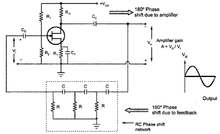
Circuit Diagram for RC-Phase Shift Oscillator using JFET

The circuit implements the RC phase shift oscillator with FET. Note that the topology used for positive feedback is voltage series feedback.

Bipolar implementation

The implementation using NPN type bipolar transistor is based on example from popular electronics hobby magazine. The circuit generates sinusoidal wave on its output. The RC phase-shift network is used to form positive feedback loop. Rb and Rc resistors polarise transistor for DC current, Rs is a separating resistor. The circuit is taken from.[3]

References

  1. ↑ http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/oscphas.html
  2. ↑ Mancini, Ron (2002). Op Amps For Everyone. Dallas, Texas: Texas Instruments. pp. 15–15,15–16.
  3. ↑ K.W.(Widelski?) (1984). Kalejdoskop Techniki. Warsaw, Poland: NOT Sigma.