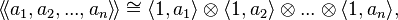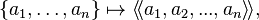Pfister form

In mathematics, a Pfister form is a particular kind of quadratic form over a field F (whose characteristic is usually assumed to be not 2), introduced by Albrecht Pfister in 1965. A Pfister form is in 2n variables, for some natural number n (also called an n-Pfister form), and may be written as a tensor product of quadratic forms as:

\langle\!\langle a_1, a_2, ... , a_n \rangle\!\rangle \cong \langle 1, a_1 \rangle \otimes \langle 1, a_2 \rangle \otimes ... \otimes \langle 1, a_n \rangle,

for ai elements of the field F. An n-Pfister form may also be constructed inductively from an (n-1)-Pfister form q and an element a of F, as 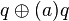q \oplus (a)q.

So all 1-Pfister forms and 2-Pfister forms look like:

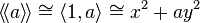\langle\!\langle a\rangle\!\rangle\cong \langle 1, a \rangle \cong x^2 + ay^2.
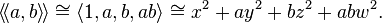
\langle\!\langle a,b\rangle\!\rangle\cong \langle 1, a, b, ab \rangle \cong x^2 + ay^2 +bz^2 +abw^2.

For n ≤ 3 the n-Pfister forms are norm forms of composition algebras.[1] In fact, in this case, two n-Pfister forms are isometric if and only if the corresponding composition algebras are isomorphic.

The Pfister forms are generators for the torsion in the Witt group.[2] The n-fold forms additively generate the n-th power In of the fundamental ideal of the Witt ring.[1]

Characterisation

We define a quadratic form q over a field F to be multiplicative if when x and y are vectors of indeterminates, then q(x).q(y) = q(z) where z is a vector of rational functions in the x and y over F. Isotropic quadratic forms are multiplicative.[3] For anisotropic quadratic forms, Pfister forms are multiplicative and conversely.[4][5]

Connection with K-theory

Let kn(F) be the n-th group in Milnor K-theory modulo 2. There are homomorphisms from kn(F) to the Witt ring by taking the symbol

\{a_1,\ldots,a_n\} \mapsto \langle\!\langle a_1, a_2, ... , a_n \rangle\!\rangle ,

where the image is an n-fold Pfister form.[6] The image can be taken as In/In+1 and the map is surjective since the Pfister forms additively generate In. The Milnor conjecture can be interpreted as stating that these maps are isomorphisms.[6]

Pfister neighbours

A Pfister neighbour is a form (W,σ) such that (W,σ) is similar to a subspace of a space with Pfister form (V,φ) where dim.V < 2 dim.W.[7] The associated Pfister form φ is uniquely determined by σ. Any ternary form is a Pfister neighbour; a quaternary form is a Pfister neighbour if and only if its discriminant is a square.[8] A degree five form is a Pfister neighbour if and only if the underlying field is a linked field.[9]

Notes

  1. ↑ 1.0 1.1 Lam (2005) p.316
  2. ↑ Lam (2005) p.395
  3. ↑ Lam (2005) p.324
  4. ↑ Lam (2005) p.325
  5. ↑ Rajwade (1993) p.164
  6. ↑ 6.0 6.1 Lam (2005) p.366
  7. ↑ Lam (2005) p.339
  8. ↑ Lam (2005) p.341
  9. ↑ Lam (2005) p.342

References

Further reading