Petzval field curvature

Optical aberration
Defocus

Tilt
Spherical aberration
Astigmatism
Coma
Distortion
Petzval field curvature
Chromatic aberration

Not to be confused with flat-field correction, which refers to brightness uniformity.
Field curvature: the image "plane" (the arc) deviates from a flat surface (the vertical line).

Petzval field curvature, named for Joseph Petzval,[1] describes the optical aberration in which a flat object normal to the optical axis (or a non-flat object past the hyperfocal distance) cannot be brought into focus on a flat image plane.

Analysis

The image-sensor array of the Kepler space observatory is curved to compensate for the telescope's Petzval curvature.

Consider an "ideal" single-element lens system for which all planar wave fronts are focused to a point at distance f from the lens. Placing this lens the distance f from a flat image sensor, image points near the optical axis will be in perfect focus, but rays off axis will come into focus before the image sensor, dropping off by the cosine of the angle they make with the optical axis. This is less of a problem when the imaging surface is spherical, as in the human eye.

Most current photographic lenses are designed to minimize field curvature, and so effectively have a focal length that increases with ray angle. The Petzval lens is one design which has significant amount of field curvature, images taken with the lens are very sharp in the centre, but at greater angles the image is out of focus. Film cameras, may be able to bend their image planes to compensate, particularly when the lens is fixed and known. This also includes plate film, which could still be bent slightly. Digital sensors are difficult to bend, although experimental products have been produced and may be released in the near-future.[2] Large mosaics of sensors (necessary anyway due to limited chip sizes) can be shaped to simulate a bend over larger scales.

The Petzval field curvature is equal to the Petzval sum over an optical system,

\sum_i \frac{n_{i+1} - n_i}{r_i n_{i+1} n_i},

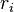where r_i is the radius of the i th surface and the n s are the indices of refraction on the first and second side of the surface.[3]

See also

References

  1. ↑ Riedl, Max J. (2001). Optical Design Fundamentals for Infrared Systems. SPIE Press. pp. 40–. ISBN 9780819440518. Retrieved 3 November 2012.
  2. ↑ . News Sony's curved sensors may allow for simpler lenses and better images. Dpreview.com. Retrieved on 2014-06-18.
  3. ↑ Kingslake, Rudolf (1989). A History of the Photographic Lens. Academic Press. pp. 4–. ISBN 9780124086401. Retrieved 3 November 2012.

External links