Peter Keevash
| Peter Keevash | |
|---|---|
| Born |
30 November 1978 Brighton, England |
| Residence | Oxford, England |
| Nationality | British |
| Fields | Mathematics |
| Institutions |
California Institute of Technology Queen Mary, University of London University of Oxford |
| Alma mater | Trinity College, Cambridge |
| Doctoral advisor | Benny Sudakov |
| Notable awards | European Prize in Combinatorics (2009) |
Peter Keevash (born 30 November 1978) is a British mathematician, specializing in combinatorics. He is a professor of mathematics at the University of Oxford, and a Fellow of Mansfield College.
Early years
Peter Keevash was born in Brighton, England, but mostly grew up in Leeds. He competed in the International Mathematical Olympiad in 1995.[1] He entered Trinity College, University of Cambridge in 1995 and completed his B.A. in mathematics in 1998. He earned his doctorate from Princeton University with Benny Sudakov as advisor. He took a postdoctoral position at the California Institute of Technology before moving to Queen Mary, University of London as a lecturer, and subsequently professor, before his move to Oxford in September 2013.
Mathematics
Keevash has published many results in combinatorics, particularly in extremal graph and hypergraph theory and Ramsey Theory. In joint work with Tom Bohman[2] he established the best-known lower bound for the off-diagonal Ramsey Number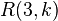 
, namely 
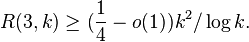(This result was obtained independently at the same time by Fiz Pontiveros, Griffiths and Morris.[3])
In early 2014 he released a preprint [4] establishing the existence of Block designs with arbitrary parameters, provided only that the underlying set is sufficiently large and satisfies certain obviously necessary divisibility conditions. In particular, his work provides the first examples of Steiner systems with parameter t ≥ 6 (and in fact provides such systems for all t).