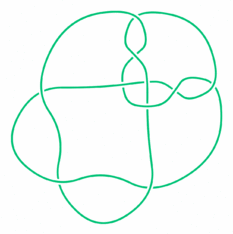
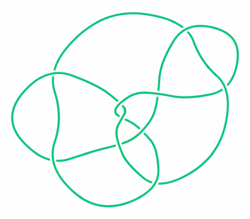
Perko pair

In the mathematical theory of knots, the Perko pair, named after Kenneth Perko, is a pair of entries in classical knot tables that actually represent the same knot. In Rolfsen's knot table, this supposed pair of distinct knots is labeled 10₁₆₁ and 10₁₆₂. In 1973, while working to complete the Tait–Little knot tables of knots up to 10 crossings (dating from the late 19th century), Perko found the duplication in C. N. Little's table. This duplication had been missed by John Horton Conway several years before in his knot table and subsequently found its way into Rolfsen's table. The Perko pair gives a counterexample to a "theorem" claimed by Little in 1900 that the writhe of a reduced diagram of a knot is an invariant.

• The Perko pair
• 

  10₁₆₁
• 

  10₁₆₂

References

• C.N. Little, Non-alternating +/- knots, Trans. Roy. Soc. Edinburgh 39 (1900), page 774
• Kenneth A. Perko Jr.(b.1943), On the classification of knots. Proc. Amer. Math. Soc. 45 (1974), 262—266.
• Dale Rolfsen, Knots and Links (see Appendix C for the knot table), 1976, ISBN 0-914098-16-0

External links

• "10_161", The Knot Atlas.
• The Revenge of the Perko Pair. Richard Elwes points out a common mistake in describing the Perko pair.