Pentagonal hexecontahedron
| Pentagonal hexecontahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | gD |
| Face type | V3.3.3.3.5 irregular pentagon |
| Faces | 60 |
| Edges | 150 |
| Vertices | 92 |
| Vertices by type | 12 {5} 20+60 {3} |
| Symmetry group | I, ½H3, [5,3]+, (532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 153° 10' 43" |
| Properties | convex, face-transitive chiral |
 Snub dodecahedron (dual polyhedron) |
 Net |
In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images (or "enantiomorphs") of each other. It is also well-known to be the Catalan solid with the most vertices. Among the Catalan and Archimedean solids, it has the second largest number of vertices, after the truncated icosidodecahedron, which has 120 vertices.
Orthogonal projections
The pentagonal hexecontahedron has three symmetry positions, two on vertices, and one mid-edge.
| Projective symmetry |
[3] | [5]+ | [2] |
|---|---|---|---|
| Image |  |
 |
 |
| Dual image |
 |
 |
 |
Related polyhedra and tilings

| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
| {5,3} | t{5,3} | r{5,3} | 2t{5,3}=t{3,5} | 2r{5,3}={3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||
 |
 |
 |
 |
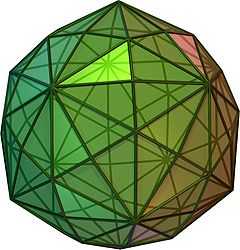 |
 | ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
This polyhedron is topologically related as a part of sequence of polyhedra and tilings of pentagons with face configurations (V3.3.3.3.n). (The sequence progresses into tilings the hyperbolic plane to any n.) These face-transitive figures have (n32) rotational symmetry.
| Symmetry n32 [n,3]+ |
Spherical | Euclidean | Compact hyperbolic | Paracompact | ||||
|---|---|---|---|---|---|---|---|---|
| 232 [2,3]+ D3 |
332 [3,3]+ T |
432 [4,3]+ O |
532 [5,3]+ I |
632 [6,3]+ P6 |
732 [7,3]+ |
832 [8,3]+... |
∞32 [∞,3]+ | |
| Snub figure |
 3.3.3.3.2 |
 3.3.3.3.3 |
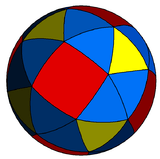 3.3.3.3.4 |
 3.3.3.3.5 |
 3.3.3.3.6 |
 3.3.3.3.7 |
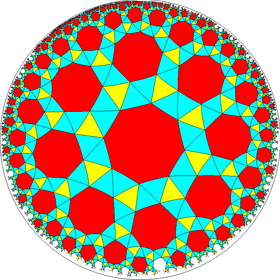 3.3.3.3.8 |
 3.3.3.3.∞ |
| Coxeter Schläfli |
sr{2,3} |
sr{3,3} |
sr{4,3} |
sr{5,3} |
sr{6,3} |
sr{7,3} |
sr{8,3} |
sr{∞,3} |
| Snub dual figure |
 V3.3.3.3.2 |
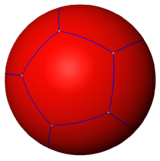 V3.3.3.3.3 |
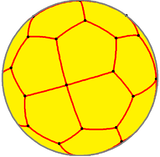 V3.3.3.3.4 |
 V3.3.3.3.5 |
 V3.3.3.3.6 |
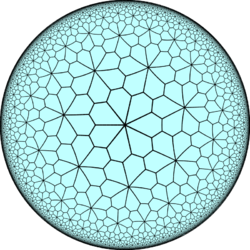 V3.3.3.3.7 |
V3.3.3.3.8 |  V3.3.3.3.∞ |
| Coxeter | ||||||||
References
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208 (The thirteen semiregular convex polyhedra and their duals, Page 29, Pentagonal hexecontahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 287, pentagonal hexecontahedron )
External links
- Eric W. Weisstein, Pentagonal hexecontahedron (Catalan solid) at MathWorld
- Pentagonal Hexecontrahedron – Interactive Polyhedron Model
| ||||||||||||||||||||||||||||||||||||