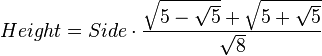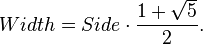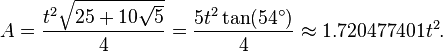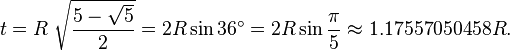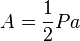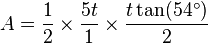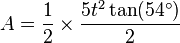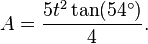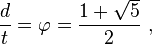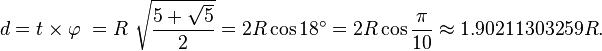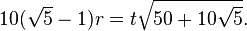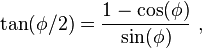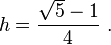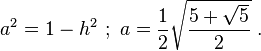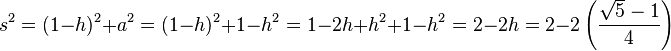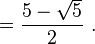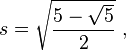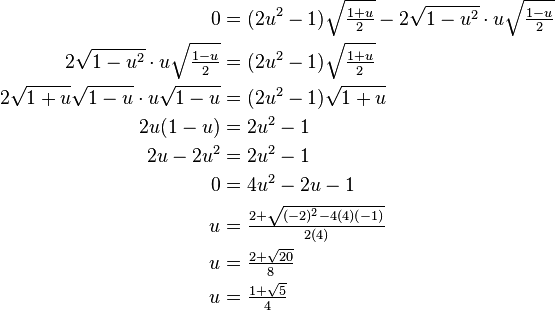Pentagon

This article is about the geometric figure. For the headquarters of the United States Department of Defense, see The Pentagon. For other uses, see Pentagon (disambiguation).

Regular pentagon
A regular pentagon
Type	Regular polygon
Edges and vertices	5
Schläfli symbol	{5}
Coxeter diagram
Symmetry group	Dihedral (D₅), order 2×5
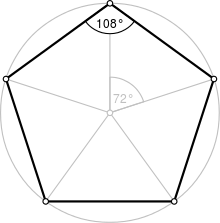
Internal angle (degrees)	108°
Dual polygon	self
Properties	convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a pentagon (from the Greek pente and gonia, meaning five and angle^[1]) is any five-sided polygon. The sum of the internal angles in a simple pentagon is 540°.

A regular pentagon has Schläfli symbol {5} and interior angles are 108°.

A pentagon may be simple or self-intersecting. A self-intersecting regular pentagon (or star pentagon) is called a pentagram.

Regular pentagons

A regular pentagon has five lines of reflectional symmetry, and rotational symmetry of order 5 (through 72°, 144°, 216° and 288°). The diagonals of a regular pentagon are in golden ratio to its sides.

Height = Side\cdot\frac{\sqrt{5-\sqrt5}+\sqrt{5+\sqrt5}}{\sqrt8}

Width = Side\cdot\frac{1+\sqrt5}{2}.

The area of a regular convex pentagon with side length t is given by

A = \frac{{t^2 \sqrt {25 + 10\sqrt 5 } }}{4} = \frac{5t^2 \tan(54^\circ)}{4} \approx 1.720477401 t^2.

A pentagram or pentangle is a regular star pentagon. Its Schläfli symbol is {5/2}. Its sides form the diagonals of a regular convex pentagon – in this arrangement the sides of the two pentagons are in the golden ratio.

When a regular pentagon is inscribed in a circle with radius R, its edge length t is given by the expression

t = R\ {\sqrt { \frac {5-\sqrt{5}}{2}} } = 2R\sin 36^\circ = 2R\sin\frac{\pi}{5} \approx 1.17557050458 R.

Derivation of the area formula

The area of any regular polygon is:

A = \frac{1}{2}Pa

where P is the perimeter of the polygon, a is the apothem. One can then substitute the respective values for P and a, which makes the formula:

A = \frac{1}{2} \times \frac{5t}{1} \times \frac{t\tan(54^\circ)}{2}

with t as the given side length. Then we can then rearrange the formula as:

A = \frac{1}{2} \times \frac{5t^2\tan(54^\circ)}{2}

and then, we combine the two terms to get the final formula, which is:

A = \frac{5t^2\tan(54^\circ)}{4}.

Derivation of the diagonal length formula

The diagonals of a regular pentagon (here represented by d) can be calculated based upon the golden ratio φ and the known side t (see discussion of the pentagon in Golden ratio):

\frac {d}{t} = \varphi = \frac {1+ \sqrt {5} }{2} \ ,

Accordingly:

d = t \times \varphi \ = R\ {\sqrt { \frac {5+\sqrt{5}}{2}} } = 2R\cos 18^\circ = 2R\cos\frac{\pi}{10} \approx 1.90211303259 R.

Inradius

The apothem, or radius r of the inscribed circle, of a regular pentagon is related to the side length t by

10(\sqrt{5}-1)r=t\sqrt{50+10\sqrt{5}}.

Chords from the circumscribing circle to the vertices

If a regular pentagon with successive vertices A, B, C, D, E is inscribed in a circle, and if P is any point on that circle between points B and C, then PA + PD = PB + PC + PE.

Construction of a regular pentagon

A variety of methods are known for constructing a regular pentagon. Some are discussed below.

Richmond's method

One method to construct a regular pentagon in a given circle is described by Richmond^[2] and further discussed in Cromwell's "Polyhedra."^[3]

The top panel shows the construction used in Richmond's method to create the side of the inscribed pentagon. The circle defining the pentagon has unit radius. Its center is located at point C and a midpoint M is marked halfway along its radius. This point is joined to the periphery vertically above the center at point D. Angle CMD is bisected, and the bisector intersects the vertical axis at point Q. A horizontal line through Q intersects the circle at point P, and chord PD is the required side of the inscribed pentagon.

To determine the length of this side, the two right triangles DCM and QCM are depicted below the circle. Using Pythagoras' theorem and two sides, the hypotenuse of the larger triangle is found as 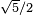$\scriptstyle \sqrt{5}/2$ . Side h of the smaller triangle then is found using the half-angle formula:

\tan ( \phi/2) = \frac{1-\cos(\phi)}{\sin (\phi)} \ ,

where cosine and sine of ϕ are known from the larger triangle. The result is:

h = \frac{\sqrt 5 - 1}{4} \ .

With this side known, attention turns to the lower diagram to find the side s of the regular pentagon. First, side a of the right-hand triangle is found using Pythagoras' theorem again:

a^2 = 1-h^2 \ ; \ a = \frac{1}{2}\sqrt { \frac {5+\sqrt 5}{2}} \ .

Then s is found using Pythagoras' theorem and the left-hand triangle as:

s^2 = (1-h)^2 + a^2 = (1-h)^2 + 1-h^2 = 1-2h+h^2 + 1-h^2 = 2-2h=2-2\left(\frac{\sqrt 5 - 1}{4}\right) \

=\frac {5-\sqrt 5}{2} \ .

The side s is therefore:

s = \sqrt{ \frac {5-\sqrt 5}{2}} \ ,

a well established result.^[4] Consequently, this construction of the pentagon is valid.

Carlyle circles

See main article: Carlyle circle

Method using Carlyle circles

The Carlyle circle was invented as a geometric method to find the roots of a quadratic equation.^[5] This methodology leads to a procedure for constructing a regular pentagon. The steps are as follows:^[6]

Draw a circle in which to inscribe the pentagon and mark the center point O.
Draw a horizontal line through the center of the circle. Mark one intersection with the circle as point B.
Construct a vertical line through the center. Mark one intersection with the circle as point A.
Construct the point M as the midpoint of O and B.
Draw a circle centered at M through the point A. Mark its intersection with the horizontal line (inside the original circle) as the point W and its intersection outside the circle as the point V.
Draw a circle of radius OA and center W. It intersects the original circle at two of the vertices of the pentagon.
Draw a circle of radius OA and center V. It intersects the original circle at two of the vertices of the pentagon.
The fifth vertex is the rightmost intersection of the horizontal line with the original circle.

Steps 6-8 are equivalent to the following version, shown in the animation:

6a. Construct point F as the midpoint of O and W.

7a. Construct a vertical line through F. It intersects the original circle at two of the vertices of the pentagon. The third vertex is the rightmost intersection of the horizontal line with the original circle.

8a. Construct the other two vertices using the compass and the length of the vertex found in step 7a.

Using trigonometry and the Pythagorean Theorem

Using trigonometry and the Pythagorean Theorem to construct a regular pentagon.

The construction

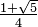We first note that a regular pentagon can be divided into 10 congruent triangles as shown in the Observation. Also, cos 36° = $\tfrac{1+\sqrt{5}}{4}$ .†
In Step 1, we use four units (shown in blue) and a right angle to construct a segment of length 1+√5, specifically by creating a 1-2-√5 right triangle and then extending the hypotenuse of √5 by a length of 1. We then bisect that segment – and then bisect again – to create a segment of length 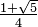$\tfrac{1+\sqrt{5}}{4}$ (shown in red.)
In Step 2, we construct two concentric circles centered at O with radii of length 1 and length 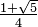$\tfrac{1+\sqrt{5}}{4}$ . We then place P arbitrarily on the smaller circle, as shown. Constructing a line perpendicular to OP passing through P, we construct the first side of the pentagon by using the points created at the intersection of the tangent and the unit circle. Copying that length four times along the outer edge of the unit circles gives us our regular pentagon.

† Proof that cos 36° = 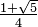$\tfrac{1+\sqrt{5}}{4}$

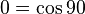
0 = \cos 90

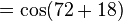
= \cos (72+18)

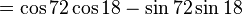= \cos 72\cos 18 - \sin 72\sin 18

(using the angle addition formula for cosine)

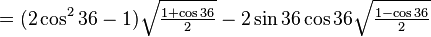= (2\cos ^2 36 -1)\sqrt{\tfrac{1+\cos 36}{2}}-2\sin 36\cos 36\sqrt{\tfrac{1-\cos 36}{2}}

(using double and half angle formulas)

Let u = cos 36. First, note that 0 < u < 1 (which will help us simplify as we work.) Now,

\begin{align} 0 & {} = (2u^2 -1)\sqrt{\tfrac{1+u}{2}}-2\sqrt{1-u^2}\cdot u\sqrt{\tfrac{1-u}{2}} \\ 2\sqrt{1-u^2}\cdot u\sqrt{\tfrac{1-u}{2}} & {} = (2u^2 -1)\sqrt{\tfrac{1+u}{2}} \\ 2\sqrt{1+u}\sqrt{1-u}\cdot u\sqrt{1-u} & {} = (2u^2 -1)\sqrt{1+u} \\ 2u(1-u) & {} = 2u^2-1 \\ 2u-2u^2 & {} = 2u^2-1 \\ 0 & {} = 4u^2-2u-1 \\ u & {} = \tfrac{2+\sqrt{(-2)^2-4(4)(-1)}}{2(4)} \\ u & {} = \tfrac{2+\sqrt{20}}{8} \\ u & {} = \tfrac{1+\sqrt{5}}{4} \end{align}

Another method

Animation of this method

Another method is this:

Draw a circle in which to inscribe the pentagon and mark the center point O. (This is the green circle in the diagram to the right).
Choose a point A on the circle that will serve as one vertex of the pentagon. Draw a line through O and A.
Construct a line perpendicular to the line OA passing through O. Mark its intersection with one side of the circle as the point B.
Construct the point C as the midpoint of the line OB.
Draw a circle centered at C through the point A. Mark its intersection with the line OB (inside the original circle) as the point D.
Draw a circle centered at A through the point D. Mark its intersections with the original (green) circle as the points E and F.
Draw a circle centered at E through the point A. Mark its other intersection with the original circle as the point G.
Draw a circle centered at F through the point A. Mark its other intersection with the original circle as the point H.
Construct the regular pentagon AEGHF.

Euclid's method

A regular pentagon is constructible using a compass and straightedge, either by inscribing one in a given circle or constructing one on a given edge. This process was described by Euclid in his Elements circa 300 BC.^[7]

Simply using a protractor (not a classical construction)

A direct method using degrees follows:

Draw a circle and choose a point to be the pentagon's (e.g. top center)
Choose a point A on the circle that will serve as one vertex of the pentagon. Draw a line through O and A.
Draw a guideline through it and the circle's center
Draw lines at 54° (from the guideline) intersecting the pentagon's point
Where those intersect the circle, draw lines at 18° (from parallels to the guideline)
Join where they intersect the circle

After forming a regular convex pentagon, if one joins the non-adjacent corners (drawing the diagonals of the pentagon), one obtains a pentagram, with a smaller regular pentagon in the center. Or if one extends the sides until the non-adjacent sides meet, one obtains a larger pentagram. The accuracy of this method depends on the accuracy of the protractor used to measure the angles.

Physical methods

Overhand knot of a paper strip

A regular pentagon may be created from just a strip of paper by tying an overhand knot into the strip and carefully flattening the knot by pulling the ends of the paper strip. Folding one of the ends back over the pentagon will reveal a pentagram when backlit.
Construct a regular hexagon on stiff paper or card. Crease along the three diameters between opposite vertices. Cut from one vertex to the center to make an equilateral triangular flap. Fix this flap underneath its neighbor to make a pentagonal pyramid. The base of the pyramid is a regular pentagon.

Cyclic pentagons

A cyclic pentagon is one for which a circle called the circumcircle goes through all five vertices. The regular pentagon is an example of a cyclic pentagon. The area of a cyclic pentagon, whether regular or not, can be expressed as one fourth the square root of one of the roots of a septic equation whose coefficients are functions of the sides of the pentagon.^[8]^[9]^[10]

There exist cyclic pentagons with rational sides and rational area; these are called Robbins pentagons. In a Robbins pentagon, either all diagonals are rational or all are irrational, and it is conjectured that all the diagonals must be rational.^[11]

General convex pentagons

For all convex pentagons, the sum of the squares of the diagonals is less than 3 times the sum of the squares of the sides.^[12]^:p.75,#1854

Graphs

The K₅ complete graph is often drawn as a regular pentagon with all 10 edges connected. This graph also represents an orthographic projection of the 5 vertices and 10 edges of the 5-cell. The rectified 5-cell, with vertices at the mid-edges of the 5-cell is projected inside a pentagon.

5-cell (4D)	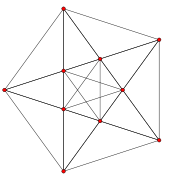Rectified 5-cell (4D)

Examples of pentagons

Plants

Pentagonal cross-section of okra.
Morning glories, like many other flowers, have a pentagonal shape.
The gynoecium of an apple contains five carpels, arranged in a five-pointed star
Starfruit is another fruit with fivefold symmetry.

Animals

A sea star. Many echinoderms have fivefold radial symmetry.
An illustration of brittle stars, also echinoderms with a pentagonal shape.

Artificial

The Pentagon, headquarters of the United States Department of Defense.
Home plate of a baseball field

Pentagons in tiling

Main article: Pentagon tiling

The best known packing of equal-sized regular pentagons on a plane is a double lattice structure which covers 92.131% of the plane.

A pentagon cannot appear in any tiling made by regular polygons. To prove a pentagon cannot form a regular tiling (one in which all faces are congruent), observe that 360 / 108 = 3¹⁄₃, which is not a whole number. More difficult is proving a pentagon cannot be in any edge-to-edge tiling made by regular polygons:

There are no combinations of regular polygons with 4 or more meeting at a vertex that contain a pentagon. For combinations with 3, if 3 polygons meet at a vertex and one has an odd number of sides, the other 2 must be congruent. The reason for this is that the polygons that touch the edges of the pentagon must alternate around the pentagon, which is impossible because of the pentagon's odd number of sides. For the pentagon, this results in a polygon whose angles are all (360 − 108) / 2 = 126°. To find the number of sides this polygon has, the result is 360 / (180 − 126) = 6²⁄₃, which is not a whole number. Therefore, a pentagon cannot appear in any tiling made by regular polygons.

Pentagons in polyhedra


Dodecahedron	Pyritohedron	Pentagonal icositetrahedron	Pentagonal hexecontahedron	Truncated trapezohedron

In-line notes and references

↑ "pentagon, adj. and n." OED Online. Oxford University Press, June 2014. Web. 17 August 2014.
↑ Herbert W Richmond (1893). "Pentagon".
↑ Peter R. Cromwell. Polyhedra. p. 63. ISBN 0-521-66405-5.
↑ This result agrees with Herbert Edwin Hawkes, William Arthur Luby, Frank Charles Touton (1920). "Exercise 175". Plane geometry. Ginn & Co. p. 302.
↑ Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. p. 329. ISBN 1-58488-347-2.
↑ Duane W DeTemple (1991). "Carlyle Circles and the Lemoine Simplicity of Polygon Constructions" (PDF). The American Mathematical Monthly 98 (2): 97–108. doi:10.2307/2323939. JSTOR link
↑ George Edward Martin (1998). Geometric constructions. Springer. p. 6. ISBN 0-387-98276-0.
↑ Weisstein, Eric W. "Cyclic Pentagon." From MathWorld--A Wolfram Web Resource.
↑ Robbins, D. P. "Areas of Polygons Inscribed in a Circle." Discr. Comput. Geom. 12, 223-236, 1994.
↑ Robbins, D. P. "Areas of Polygons Inscribed in a Circle." Amer. Math. Monthly 102, 523-530, 1995.
↑
- Buchholz, Ralph H.; MacDougall, James A. (2008), "Cyclic polygons with rational sides and area", Journal of Number Theory 128 (1): 17–48, doi:10.1016/j.jnt.2007.05.005, MR 2382768 .
↑ Inequalities proposed in “Crux Mathematicorum”, .

External links

Look up pentagon in Wiktionary, the free dictionary.

Weisstein, Eric W., "Pentagon", MathWorld.
Animated demonstration constructing an inscribed pentagon with compass and straightedge.
How to construct a regular pentagon with only a compass and straightedge.
How to fold a regular pentagon using only a strip of paper
Definition and properties of the pentagon, with interactive animation
Renaissance artists' approximate constructions of regular pentagons
Pentagon. How to calculate various dimensions of regular pentagons.

Regular polygons

Listed by number of sides

1–10 sides	Monogon Digon Equilateral triangle Square Pentagon Hexagon Heptagon Octagon Nonagon (Enneagon) Decagon

11–20 sides	Hendecagon Dodecagon Tridecagon Tetradecagon Pentadecagon Hexadecagon Heptadecagon Octadecagon Enneadecagon Icosagon

24, 30–100 sides	Icositetragon Triacontagon Tetracontagon Pentacontagon Hexacontagon Heptacontagon Octacontagon Enneacontagon Hectogon

Others	257-gon Chiliagon Myriagon 65537-gon Megagon Apeirogon

Star polygons (5–12 sides)	Pentagram Hexagram Heptagram Octagram Enneagram Decagram Hendecagram Dodecagram