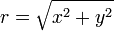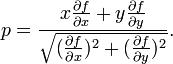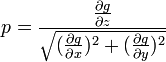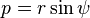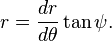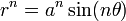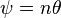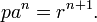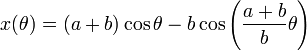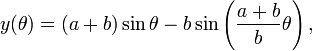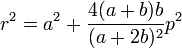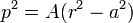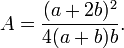Pedal equation

For a plane curve C and a given fixed point O, the pedal equation of the curve is a relation between r and p where r is the distance from O to a point on C and p is the perpendicular distance from O to the tangent line to C at the point. The point O is called the pedal point and the values r and p are sometimes called the pedal coordinates of a point relative to the curve and the pedal point. Some curves have particularly simple pedal equations and knowing the pedal equation of a curve may simplify the calculation of certain of its properties such as curvature.

Equations

Cartesian coordinates

For C given in rectangular coordinates by f(x, y) = 0, and with O taken to be the origin, the pedal coordinates of the point (x, y) are given by:^[1]

r=\sqrt{x^2+y^2}

p=\frac{x\frac{\partial f}{\partial x}+y\frac{\partial f}{\partial y}}{\sqrt{(\frac{\partial f}{\partial x})^2+(\frac{\partial f}{\partial y})^2}}.

The pedal equation can be found by eliminating x and y from these equations and the equation of the curve.

The expression for p may be simplified if the equation of the curve is written in homogeneous coordinates by introducing a variable z, so that the equation of the curve is g(x, y, z) = 0. The value of p is then given by^[2]

p=\frac{\frac{\partial g}{\partial z}}{\sqrt{(\frac{\partial g}{\partial x})^2+(\frac{\partial g}{\partial y})^2}}

where the result is evaluated at z=1

Polar coordinates

For C given in polar coordinates by r = f(θ), then

p=r\sin \psi\,

where ψ is the polar tangential angle given by

r=\frac{dr}{d\theta}\tan \psi.

The pedal equation can be found by eliminating θ from these equations.^[3]

Pedal equations for specific curves

Sinusoidal spirals

For a sinusoidal spiral written in the form

r^n = a^n \sin(n \theta)\,

the polar tangential angle is

\psi = n\theta

which produces the pedal equation

pa^n=r^{n+1}.

The pedal equation for a number of familiar curves can be obtained setting n to specific values:^[4]

n	Curve	Pedal point	Pedal eq.
1	Circle with radius a	Point on circumference	pa = r²
−1	Line	Point distance a from line	p = a
¹⁄₂	Cardioid	Cusp	p²a = r³
−¹⁄₂	Parabola	Focus	p² = ar
2	Lemniscate of Bernoulli	Center	pa² = r³
−2	Rectangular hyperbola	Center	rp = a²

Epi- and hypocycloids

For a epi- or hypocycloid given by parametric equations

x (\theta) = (a + b) \cos \theta - b \cos \left( \frac{a + b}{b} \theta \right)

y (\theta) = (a + b) \sin \theta - b \sin \left( \frac{a + b}{b} \theta \right),

the pedal equation with respect to the origin is^[5]

r^2=a^2+\frac{4(a+b)b}{(a+2b)^2}p^2

or^[6]

p^2=A(r^2-a^2)

with

A=\frac{(a+2b)^2}{4(a+b)b}.

Special cases obtained by setting b=^a⁄_n for specific values of n include:

n	Curve	Pedal eq.
1, −¹⁄₂	Cardioid	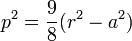$p^2=\frac{9}{8}(r^2-a^2)$
2, −²⁄₃	Nephroid	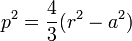$p^2=\frac{4}{3}(r^2-a^2)$
−3, −³⁄₂	Deltoid	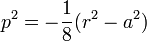$p^2=-\frac{1}{8}(r^2-a^2)$
−4, −⁴⁄₃	Astroid	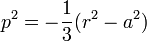$p^2=-\frac{1}{3}(r^2-a^2)$

Other curves

Other pedal equations are:^[7]

Curve	Equation	Pedal point	Pedal eq.
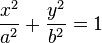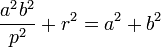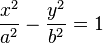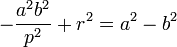Ellipse	$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$	Center	$\frac{a^2b^2}{p^2}+r^2=a^2+b^2$
Hyperbola	$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$	Center	$-\frac{a^2b^2}{p^2}+r^2=a^2-b^2$
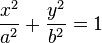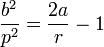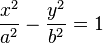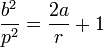Ellipse	$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$	Focus	$\frac{b^2}{p^2}=\frac{2a}{r}-1$
Hyperbola	$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$	Focus	$\frac{b^2}{p^2}=\frac{2a}{r}+1$
Logarithmic spiral	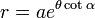$r = ae^{\theta \cot \alpha}\,$	Pole	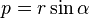$p=r \sin \alpha$