Paving matroid

In the mathematical theory of matroids, a paving matroid is a matroid in which every circuit has size at least as large as the matroid's rank. In a matroid of rank  every circuit has size at most
every circuit has size at most 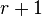 , so it is equivalent to define paving matroids as the matroids in which the size of every circuit belongs to the set
, so it is equivalent to define paving matroids as the matroids in which the size of every circuit belongs to the set 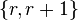 .[1]
.[1]
Examples
Every simple matroid of rank three is a paving matroid; for instance this is true of the Fano matroid. Combinatorial enumeration of the simple matroids on up to nine elements has shown that a large fraction of them are also paving matroids.[1] The Vámos matroid provides another example, of rank four.
Uniform matroids of rank  have the property that every circuit is of length exactly
have the property that every circuit is of length exactly 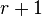 and hence are all paving matroids;[2] the converse does not hold, for example, the cycle matroid of the complete graph
and hence are all paving matroids;[2] the converse does not hold, for example, the cycle matroid of the complete graph 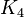 is paving but not uniform.[3]
is paving but not uniform.[3]
A Steiner system 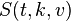 is a pair
is a pair 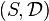 where
where  is a finite set of size
is a finite set of size 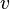 and
and 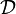 is a family of
is a family of 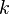 -element subsets of
-element subsets of  with the property that every
with the property that every 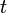 -element subset of
-element subset of  is also a subset of exactly one set in
is also a subset of exactly one set in 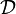 . The elements of
. The elements of 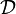 form a
form a 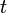 -partition of
-partition of  and hence are the hyperplanes of a paving matroid on
and hence are the hyperplanes of a paving matroid on  .[4]
.[4]
d-Partitions
If a paving matroid has rank 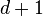 , then its hyperplanes form a set system known as a
, then its hyperplanes form a set system known as a 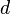 -partition. A family of two or more sets
-partition. A family of two or more sets  forms a
forms a 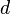 -partition if every set in
-partition if every set in  has size at least
has size at least 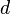 and every
and every 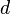 -element subset of
-element subset of 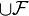 is a subset of exactly one set in
is a subset of exactly one set in  . Conversely, if
. Conversely, if  is a
is a 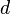 -partition, then it can be used to define a paving matroid on
-partition, then it can be used to define a paving matroid on 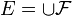 for which
for which  is the set of hyperplanes. In this matroid, a subset
is the set of hyperplanes. In this matroid, a subset 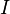 of
of 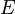 is independent whenever either
is independent whenever either 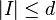 or
or 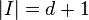 and
and 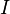 is not a subset of any set in
is not a subset of any set in  .[1]
.[1]
History
Paving matroids were initially studied by Hartmanis (1959), in their equivalent formulation in terms of 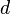 -partitions; Hartmanis called them generalized partition lattices. In their 1970 book Combinatorial Geometries, Henry Crapo and Gian-Carlo Rota observed that these structures were matroidal; the name "paving matroid" was introduced by Welsh (1976) following a suggestion of Rota.[5]
-partitions; Hartmanis called them generalized partition lattices. In their 1970 book Combinatorial Geometries, Henry Crapo and Gian-Carlo Rota observed that these structures were matroidal; the name "paving matroid" was introduced by Welsh (1976) following a suggestion of Rota.[5]
The simpler structure of paving matroids, compared to arbitrary matroids, has allowed some facts about them to be proven that remain elusive in the more general case. An example is Rota's basis conjecture, the statement that a set of n disjoint bases in a rank-n matroid can be arranged into an n × n matrix so that the rows of the matrix are the given bases and the columns are also bases. It has been proven true for paving matroids, but remains open for most other matroids.[6]
Notes
- ↑ 1.0 1.1 1.2 Welsh (2010).
- ↑ Oxley 1992, p. 26
- ↑ Oxley 1992, p. 27
- ↑ Oxley 1992, p. 367
- ↑ Oxley 1992, p. 75
- ↑ Geelen & Humphries (2006).
References
- Geelen, Jim; Humphries, Peter J. (2006), "Rota's basis conjecture for paving matroids", SIAM Journal on Discrete Mathematics 20 (4): 1042–1045 (electronic), doi:10.1137/060655596, MR 2272246.
- Hartmanis, Juris (1959), "Lattice theory of generalized partitions", Canadian Journal of Mathematics 11: 97–106, doi:10.4153/CJM-1959-013-8, MR 0099931, Zbl 0089.37002.
- Oxley, James G. (1992), Matroid theory, Oxford Science Publications, Oxford: Oxford University Press, ISBN 0-19-853563-5, Zbl 0784.05002
- Welsh, D. J. A. (2010) [1976], "2.3. Paving Matroids", Matroid Theory, Courier Dover Publications, pp. 40–41, 44, ISBN 9780486474397.