Pasting lemma

In topology, the pasting lemma is an important result which says that two continuous functions can be "glued together" to create another continuous function. The lemma is implicit in the use of piecewise functions. It is also called the gluing rule. 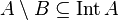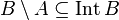for example in the book Topology and Groupoids, where the more general condition for the statement below is that $A \setminus B \subseteq \operatorname{Int} A$ and $B \setminus A \subseteq \operatorname{Int} B$ .

The pasting (or gluing) lemma is crucial to the construction of the fundamental group or fundamental groupoid of a topological space; it allows one to concatenate continuous paths to create a new continuous path.

Formal statement

Let 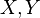$X,Y$ be both closed (or both open) subsets of a topological space A such that 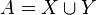$A = X \cup Y$ , and let B also be a topological space. If 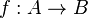$f: A \to B$ is continuous when restricted to both X and Y, then f is continuous.

This result allows one to take two continuous functions defined on closed (or open) subsets of a topological space and create a new one.

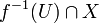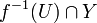Proof: if U is a closed subset of B, then $f^{-1}(U )\cap X$ and $f^{-1}(U )\cap Y$ are both closed since the intersection of two closed sets is closed, and f restricted to both X and Y is continuous. Therefore, their union, 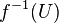$f^{-1}(U)$ is also closed. A similar argument applies when X and Y are both open. $\Box$

The infinite analog of this result (where 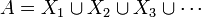$A=X_1\cup X_2\cup X_3\cup\cdots$ )is not true for closed 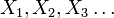$X_1, X_2, X_3\ldots$ . It is, however, true if the 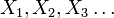$X_1, X_2, X_3\ldots$ are open; this follows from the fact that an arbitrary union of open sets is open.

References

Munkres, James; Topology, Prentice Hall; 2nd edition (December 28, 1999). ISBN 0-13-181629-2.
Dugundji, James; Topology, Allyn and Bacon; 1966. Theorem III.9.4, p.83.
Brown, Ronald; Topology and Groupoids (Booksurge) 2006 ISBN 1-4196-2722-8.