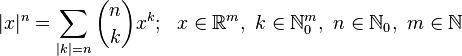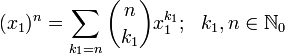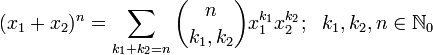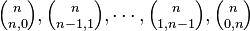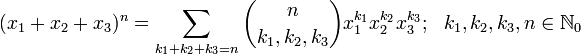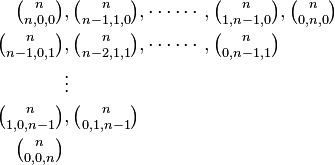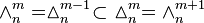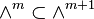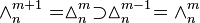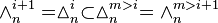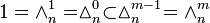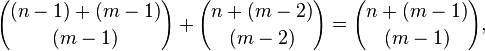Pascal's simplex

In mathematics, Pascal's simplex is a generalisation of Pascal's triangle into arbitrary number of dimensions, based on the multinomial theorem.

Generic Pascal's m-simplex

Let m (m > 0) be a number of terms of a polynomial and n (n ≥ 0) be a power the polynomial is raised to.

Let 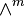$\wedge^m$ denote a Pascal's m-simplex. Each Pascal's m-simplex is a semi-infinite object, which consists of an infinite series of its components.

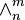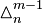Let $\wedge^m_n$ denote its n^th component, itself a finite (m − 1)-simplex with the edge length n, with a notational equivalent $\vartriangle^{m-1}_n$ .

n^th component

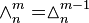$\wedge^m_n = \vartriangle^{m-1}_n$ consists of the coefficients of multinomial expansion of a polynomial with m terms raised to the power of n:

|x|^n=\sum_{|k|=n}{\binom{n}{k}x^k};\ \ x\in\mathbb{R}^m,\ k\in\mathbb{N}^m_0,\ n\in\mathbb{N}_0,\ m\in\mathbb{N}

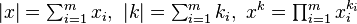where $\textstyle|x|=\sum_{i=1}^m{x_i},\ |k|=\sum_{i=1}^m{k_i},\ x^k=\prod_{i=1}^m{x_i^{k_i}}$ .

Example for 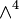$\wedge^4$

Pascal's 4-simplex (sequence A189225 in OEIS), sliced along the k₄. All points of the same color belong to the same n-th component, from red (for n = 0) to blue (for n = 3).

Specific Pascal's simplices

Pascal's 1-simplex

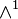$\wedge^1$ is not known by any special name.

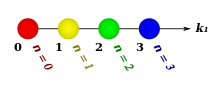
n^th component

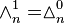$\wedge^1_n = \vartriangle^0_n$ (a point) is the coefficient of multinomial expansion of a polynomial with 1 term raised to the power of n:

(x_1)^n = \sum_{k_1=n} {n \choose k_1} x_1^{k_1};\ \ k_1, n \in \mathbb{N}_0

Arrangement of 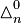$\vartriangle^0_n$

\textstyle {n \choose n}

which equals 1 for all n.

Pascal's 2-simplex

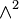$\wedge^2$ is known as Pascal's triangle (sequence A007318 in OEIS).

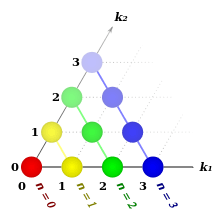
n^th component

$\wedge^2_n = \vartriangle^1_n$ (a line) consists of the coefficients of binomial expansion of a polynomial with 2 terms raised to the power of n:

(x_1 + x_2)^n = \sum_{k_1+k_2=n} {n \choose k_1, k_2} x_1^{k_1} x_2^{k_2};\ \ k_1, k_2, n \in \mathbb{N}_0

Arrangement of $\vartriangle^1_n$

\textstyle {n \choose n, 0}, {n \choose n - 1, 1}, \cdots, {n \choose 1, n - 1}, {n \choose 0, n}

Pascal's 3-simplex

$\wedge^3$ is known as Pascal's tetrahedron (sequence A046816 in OEIS).

n^th component

$\wedge^3_n = \vartriangle^2_n$ (a triangle) consists of the coefficients of trinomial expansion of a polynomial with 3 terms raised to the power of n:

(x_1 + x_2 + x_3)^n = \sum_{k_1+k_2+k_3=n} {n \choose k_1, k_2, k_3} x_1^{k_1} x_2^{k_2} x_3^{k_3};\ \ k_1, k_2, k_3, n \in \mathbb{N}_0

Arrangement of 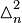$\vartriangle^2_n$

\begin{align} \textstyle {n \choose n, 0, 0} &, \textstyle {n \choose n - 1, 1, 0}, \cdots\cdots, {n \choose 1, n - 1, 0}, {n \choose 0, n, 0}\\ \textstyle {n \choose n - 1, 0, 1} &, \textstyle {n \choose n - 2, 1, 1}, \cdots\cdots, {n \choose 0, n - 1, 1}\\ &\vdots\\ \textstyle {n \choose 1, 0, n - 1} &, \textstyle {n \choose 0, 1, n - 1}\\ \textstyle {n \choose 0, 0, n} \end{align}

Properties

Inheritance of components

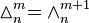$\wedge^m_n = \vartriangle^{m-1}_n$ is numerically equal to each (m − 1)-face (there is m + 1 of them) of $\vartriangle^m_n = \wedge^{m+1}_n$ , or:

\wedge^m_n = \vartriangle^{m-1}_n \subset\ \vartriangle^m_n = \wedge^{m+1}_n

From this follows, that the whole 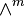$\wedge^m$ is (m + 1)-times included in 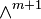$\wedge^{m+1}$ , or:

\wedge^m \subset \wedge^{m+1}

Example

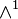
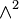
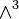
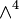
         $\wedge^1$           $\wedge^2$          $\wedge^3$           $\wedge^4$ 

 $\wedge^m_0$      1          1          1          1

 $\wedge^m_1$      1         1 1        1 1        1 1  1
                              1          1

 $\wedge^m_2$      1        1 2 1      1 2 1      1 2 1  2 2  1
                             2 2        2 2    2
                              1          1

 $\wedge^m_3$      1       1 3 3 1    1 3 3 1    1 3 3 1  3 6 3  3 3  1
                            3 6 3      3 6 3    6 6    3
                             3 3        3 3      3
                              1          1

For more terms in the above array refer to (sequence A191358 in OEIS)

Equality of sub-faces

Conversely, 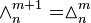$\wedge^{m+1}_n = \vartriangle^m_n$ is (m + 1)-times bounded by 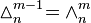$\vartriangle^{m-1}_n = \wedge^m_n$ , or:

\wedge^{m+1}_n = \vartriangle^m_n \supset \vartriangle^{m-1}_n = \wedge^m_n

From this follows, that for given n, all i-faces are numerically equal in n^th components of all Pascal's (m > i)-simplices, or:

\wedge^{i+1}_n = \vartriangle^i_n \subset \vartriangle^{m>i}_n = \wedge^{m>i+1}_n

Example

The 3rd component (2-simplex) of Pascal's 3-simplex is bounded by 3 equal 1-faces (lines). Each 1-face (line) is bounded by 2 equal 0-faces (vertices):

2-simplex   1-faces of 2-simplex         0-faces of 1-face

 1 3 3 1    1 . . .  . . . 1  1 3 3 1    1 . . .   . . . 1
  3 6 3      3 . .    . . 3    . . .
   3 3        3 .      . 3      . .
    1          1        1        .

Also, for all m and all n:

1 = \wedge^1_n = \vartriangle^0_n \subset \vartriangle^{m-1}_n = \wedge^m_n

Number of coefficients

For the n^th component ((m − 1)-simplex) of Pascal's m-simplex, the number of the coefficients of multinomial expansion it consists of is given by:

{(n-1) + (m-1) \choose (m-1)} + {n + (m - 2) \choose (m - 2)} = {n + (m - 1) \choose (m - 1)},

that is, either by a sum of the number of coefficients of an (n − 1)^th component ((m − 1)-simplex) of Pascal's m-simplex with the number of coefficients of an n^th component ((m − 2)-simplex) of Pascal's (m − 1)-simplex, or by a number of all possible partitions of an n^th power among m exponents.

Example

Number of coefficients of n^th component ((m − 1)-simplex) of Pascal's m-simplex
m-simplex	n^th component	n = 0	n = 1	n = 2	n = 3	n = 4	n = 5
1-simplex	0-simplex	1	1	1	1	1	1
2-simplex	1-simplex	1	2	3	4	5	6
3-simplex	2-simplex	1	3	6	10	15	21
4-simplex	3-simplex	1	4	10	20	35	56
5-simplex	4-simplex	1	5	15	35	70	126
6-simplex	5-simplex	1	6	21	56	126	252

Interestingly, the terms of this table comprise a Pascal triangle in the format of a symmetric Pascal matrix.

Symmetry

(An n^th component ((m − 1)-simplex) of Pascal's m-simplex has the (m!)-fold spatial symmetry.)

Geometry

(Orthogonal axes k_1 ... k_m in m-dimensional space, vertices of component at n on each axe, the tip at [0,...,0] for n=0.)

Numeric construction

(Wrapped n-th power of a big number gives instantly the n-th component of a Pascal's simplex.)

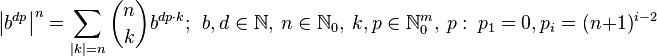
$\left|b^{dp}\right|^n=\sum_{|k|=n}{\binom{n}{k}b^{dp\cdot k}};\ \ b,d\in\mathbb{N},\ n\in\mathbb{N}_0,\ k,p\in\mathbb{N}_0^m,\ p:\ p_1=0, p_i=(n+1)^{i-2}$

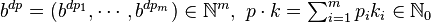where $\textstyle b^{dp} = (b^{dp_1},\cdots,b^{dp_m})\in\mathbb{N}^m,\ p\cdot k={\sum_{i=1}^m{p_i k_i}}\in\mathbb{N}_0$ .

Pascal's simplex

Generic Pascal's m-simplex

nth component

Example for

Specific Pascal's simplices

Pascal's 1-simplex

nth component

Arrangement of

Pascal's 2-simplex

nth component

Arrangement of

Pascal's 3-simplex

nth component

Arrangement of

Properties

Inheritance of components

Example

Equality of sub-faces

Example

Number of coefficients

Example

Symmetry

Geometry

Numeric construction

n^th component

Example for $\wedge^4$

n^th component

Arrangement of $\vartriangle^0_n$

n^th component

Arrangement of $\vartriangle^1_n$

n^th component

Arrangement of $\vartriangle^2_n$