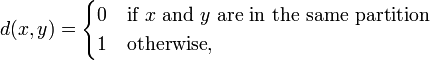Partition topology

In mathematics, the partition topology is a topology that can be induced on any set X by partitioning X into disjoint subsets P; these subsets form the basis for the topology. There are two important examples which have their own names:

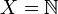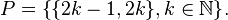
The odd–even topology is the topology where $X = \mathbb{N}$ and $P = {\left \{ \{2k-1,2k\},k\in\mathbb{N} \right \} }.$
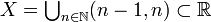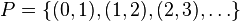The deleted integer topology is defined by letting $X = \begin{matrix}\bigcup_{n\in\mathbb{N}} (n-1,n) \subset \mathbb{R} \end{matrix}$ and $P= {\left \{ (0,1), (1,2), (2,3), \dots \right \} }$ .

The trivial partitions yield the discrete topology (each point of X is a set in P) or indiscrete topology (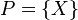 $P = \{X\}$ ).

Any set X with a partition topology generated by a partition P can be viewed as a pseudometric space with a pseudometric given by:

d(x,y) = \begin{cases} 0 & \text{if }x\text{ and }y\text{ are in the same partition} \\ 1 & \text{otherwise}, \end{cases}

This is not a metric unless P yields the discrete topology.

The partition topology provides an important example of the independence of various separation axioms. Unless P is trivial, at least one set in P contains more than one point, and the elements of this set are topologically indistinguishable: the topology does not separate points. Hence X is not a Kolmogorov space, nor a T₁ space, a Hausdorff space or an Urysohn space. In a partition topology the complement of every open set is also open, and therefore a set is open if and only if it is closed. Therefore, X is a regular, completely regular, normal and completely normal.

We note also that X/P is the discrete topology.

References

Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-486-68735-3, MR 507446