Partially ordered space

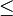In mathematics, a partially ordered space (or pospace) is a topological space $X$ equipped with a closed partial order $\leq$ , i.e. a partial order whose graph 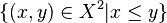$\{(x, y) \in X^2 | x \leq y\}$ is a closed subset of $X^2$ .

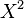From pospaces, one can define dimaps, i.e. continuous maps between pospaces which preserve the order relation.

Equivalences

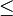For a topological space $X$ equipped with a partial order $\leq$ , the following are equivalent:

$X$ is a partially ordered space.
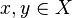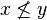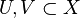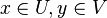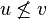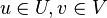For all $x,y\in X$ with $x \not\leq y$ , there are open sets $U,V\subset X$ with $x\in U, y\in V$ and $u \not\leq v$ for all $u\in U, v\in V$ .
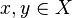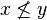For all $x,y\in X$ with $x \not\leq y$ , there are disjoint neighbourhoods $U$ of $x$ and $V$ of $y$ such that $U$ is an upper set and $V$ is a lower set.

The order topology is a special case of this definition, since a total order is also a partial order. Every pospace is a Hausdorff space. If we take equality $=$ as the partial order, this definition becomes the definition of a Hausdorff space.

Partially ordered space

Equivalences

See also