Partial order reduction
In computer science, partial order reduction is a technique for reducing the size of the state-space to be searched by a model checking algorithm. It exploits the commutativity of concurrently executed transitions, which result in the same state when executed in different orders.
In explicit state space exploration, partial order reduction usually refers to the specific technique of expanding a representative subset of all enabled transitions. This technique has also been described as model checking with representatives (Peled 1993). There are various versions of the method, the so-called stubborn set method (Valmari 1990), ample set method (Peled 1993), and persistent set method (Godefroid 1994).
Ample sets
Ample sets are an example of model checking with representatives. Their formulation relies on a separate notion of dependency. Two transitions are considered independent only if whenever they are mutually enabled, they cannot disable another and the execution of both results in a unique state regardless of the order in which they are executed. Transitions that are not independent, are dependent. In practice dependency is approximated using static analysis.
Ample sets for different purposes can be defined by giving conditions as to when a set of transitions is "ample" in a given state.
C0 
C1 If a transition  depends on some transition relation in ample(s), this transition cannot be invoked until some transition in the ample set executed.
depends on some transition relation in ample(s), this transition cannot be invoked until some transition in the ample set executed.
Conditions C0 and C1 are sufficient for preserving all the deadlocks in the state space. Further restrictions are needed in order to preserve more nuanced properties. For instance, in order to preserve properties of linear temporal logic, the following two conditions are needed:
C2 If 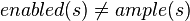 , each transition in the ample set is invisible
, each transition in the ample set is invisible
C3 A cycle is not allowed if it contains a state in which some transition  is enabled, but is never included in ample(s) for any states s on the cycle.
is enabled, but is never included in ample(s) for any states s on the cycle.
These conditions are sufficient for an ample set, but not necessary conditions (Clarke 1999).
Stubborn sets
Stubborn sets make no use of an explicit independence relation. Instead they are defined solely through commutativity over
sequences of actions. A set 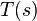 is (weakly) stubborn at s, if the following hold.
is (weakly) stubborn at s, if the following hold.
D0 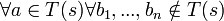 , if execution of the sequence
, if execution of the sequence 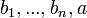 is possible and leads to the state
is possible and leads to the state 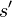 , then execution of the sequence
, then execution of the sequence 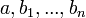 is possible and will lead to state
is possible and will lead to state 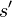
D1 Either  is a deadlock, or
is a deadlock, or 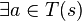 such that
such that 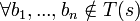 , the execution of
, the execution of 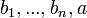 is possible.
is possible.
These conditions are sufficient for preserving all deadlocks, just like C0 and C1 are in the ample set method. They are, however, somewhat weaker, and as such may lead to smaller sets. The conditions C2 and C3 can also be further weakened from what they are in the ample set method, but the stubborn set method is compatible with C2 and C3.
Others
There are also other notations for partial order reduction. One of the commonly used is the persistent set/sleep set algorithm. Detailed information can be found in Patrice Godefroid's thesis (Godefroid 1994).
In symbolic model checking, partial order reduction can be achieved by adding more constraints (guard strengthening).
References
- Valmari, Antti (1990). "Stubborn sets for reduced state space generation". Advances in Petri Nets 1990, LNCS 483, Springer 1991. pp. 491–515.
- Peled, Doron A. (1993). "All from One, One for All: Model Checking Using Representatives". Proceedings of CAV'93, LNCS 697, Springer 1993. pp. 409–423.
- Clarke, Edmund M; Orna Grumberg and Doron A. Peled (1999). Model Checking. MIT Press.
- Godefroid, Patrice (1994). "Partial-Order Methods for the Verification of Concurrent Systems -- An Approach to the State-Explosion Problem" (PostScript) (PhD. thesis). University of Liege, Computer Science Department.
- Holzmann, Gerard J (1993). The Spin Model Checker: Primer and Reference Manual. Addison-Wesley. ISBN 0-321-22862-6.