Parikh's theorem

Parikh's theorem in theoretical computer science says that if one looks only at the relative number of occurrences of terminal symbols in a context-free language, without regard to their order, then the language is indistinguishable from a regular language.^[1] It is useful for deciding whether or not a string with a given number of some terminals is accepted by a context-free grammar.^[2] It was first proved by Rohit Parikh in 1961^[3] and republished in 1966.^[4]

Definitions and formal statement

Let 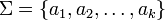$\Sigma=\{a_1,a_2,\ldots,a_k\}$ be an alphabet. The Parikh vector of a word is defined as the function 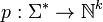$p:\Sigma^*\to\mathbb{N}^k$ , given by^[1]

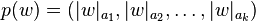$p(w)=(|w|_{a_1}, |w|_{a_2}, \ldots, |w|_{a_k})$ , where 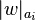$|w|_{a_i}$ denotes the number of occurrences of the letter 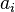$a_i$ in the word $w$ .

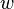A subset of 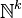$\mathbb{N}^k$ is said to be linear if it is of the form

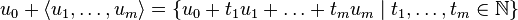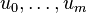$u_0+\langle u_1,\ldots,u_m\rangle=\{u_0+t_1u_1+\ldots+t_mu_m \mid t_1,\ldots,t_m\in\mathbb{N}\}$ for some vectors $u_0,\ldots,u_m$ .

A subset of 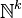$\mathbb{N}^k$ is said to be semi-linear if it is a union of finitely many linear subsets.

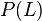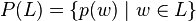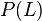The formal statement of Parikh's theorem is as follows. Let $L$ be a context-free language. Let $P(L)$ be the set of Parikh vectors of words in $L$ , that is, $P(L) = \{p(w) \mid w \in L\}$ . Then $P(L)$ is a semi-linear set.

If $S$ is any semi-linear set, the language of words whose Parikh vectors are in $S$ is a regular language. Thus, if one considers two languages to be commutatively equivalent if they have the same set of Parikh vectors, then every context-free language is commutatively equivalent to some regular language.

Significance

Parikh's theorem proves that some context-free languages can only have ambiguous grammars. Such languages are called inherently ambiguous languages. From a formal grammar perspective, this means that some ambiguous context-free grammars cannot be converted to equivalent unambiguous context-free grammars.

References

↑ 1.0 1.1 Kozen, Dexter (1997). Automata and Computability. New York: Springer-Verlag. ISBN 3-540-78105-6.
↑ Håkan Lindqvist. "Parikh's theorem". Umeå Universitet.
↑ Parikh, Rohit (1961). "Language Generating Devices". Quartly Progress Report, Research Laboratory of Electronics, MIT.
↑ Parikh, Rohit (1966). "On Context-Free Languages". Journal of the Association for Computing Machinery 13 (4).