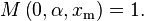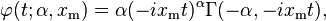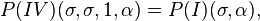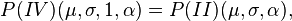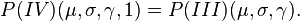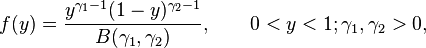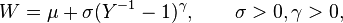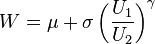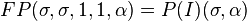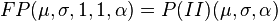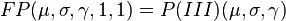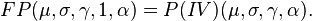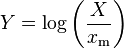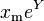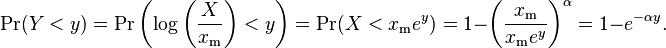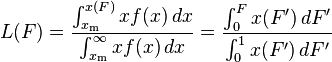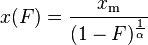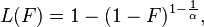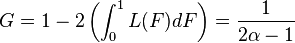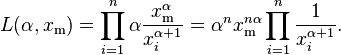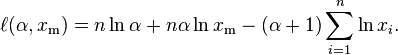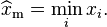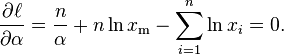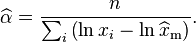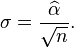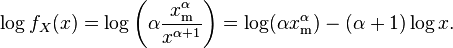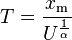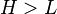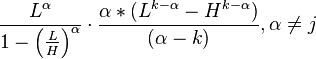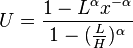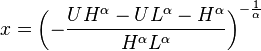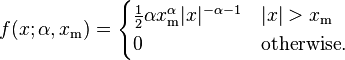Pareto distribution
|
Probability density function
| |
|
Cumulative distribution function
| |
| Parameters |
xm > 0 scale (real) α > 0 shape (real) |
|---|---|
| Support |
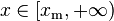 |
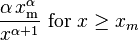 | |
| CDF |
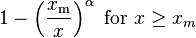 |
| Mean |
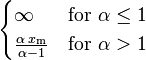 |
| Median |
![x_\mathrm{m} \sqrt[\alpha]{2}](../I/m/3c52a1728ced91e276d35d6e39be8ac3.png) |
| Mode |
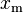 |
| Variance |
![\begin{cases}
\infty & \text{for }\alpha\in(1,2] \\
\frac{x_\mathrm{m}^2\alpha}{(\alpha-1)^2(\alpha-2)} & \text{for }\alpha>2
\end{cases}](../I/m/491564d13ae4a843032962d0667ec7aa.png) |
| Skewness |
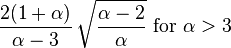 |
| Ex. kurtosis |
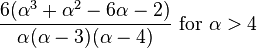 |
| Entropy |
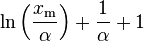 |
| MGF |
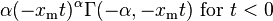 |
| CF |
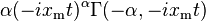 |
| Fisher information |
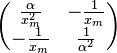 |
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power law probability distribution that is used in description of social, scientific, geophysical, actuarial, and many other types of observable phenomena.
Definition
If X is a random variable with a Pareto (Type I) distribution,[1] then the probability that X is greater than some number x, i.e. the survival function (also called tail function), is given by
where xm is the (necessarily positive) minimum possible value of X, and α is a positive parameter. The Pareto Type I distribution is characterized by a scale parameter xm and a shape parameter α, which is known as the tail index. When this distribution is used to model the distribution of wealth, then the parameter α is called the Pareto index.
Properties
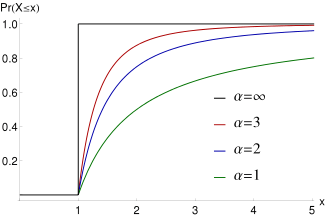
Cumulative distribution function
From the definition, the cumulative distribution function of a Pareto random variable with parameters α and xm is
When plotted on linear axes, the distribution assumes the familiar J-shaped curve which approaches each of the orthogonal axes asymptotically. All segments of the curve are self-similar (subject to appropriate scaling factors). When plotted in a log-log plot, the distribution is represented by a straight line.
Probability density function
It follows (by differentiation) that the probability density function is
Moments and characteristic function
- The expected value of a random variable following a Pareto distribution is
- The variance of a random variable following a Pareto distribution is
- (If α ≤ 1, the variance does not exist.)
- The raw moments are
- The moment generating function is only defined for non-positive values t ≤ 0 as
- The characteristic function is given by
- where Γ(a, x) is the incomplete gamma function.
Conditional distributions
The conditional probability distribution of a Pareto-distributed random variable, given the event that it is greater than or equal to a particular number  exceeding
exceeding 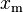 , is a Pareto distribution with the same Pareto index
, is a Pareto distribution with the same Pareto index  but with minimum
but with minimum  instead of
instead of 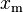 .
.
A characterization theorem
Suppose 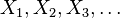 are independent identically distributed random variables whose probability distribution is supported on the interval
are independent identically distributed random variables whose probability distribution is supported on the interval 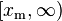 for some
for some 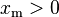 . Suppose that for all
. Suppose that for all  , the two random variables
, the two random variables 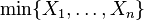 and
and 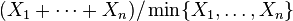 are independent. Then the common distribution is a Pareto distribution.
are independent. Then the common distribution is a Pareto distribution.
Geometric mean
The geometric mean (G) is[2]
-
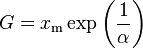 .
.
Harmonic mean
The harmonic mean (H) is[2]
-
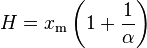 .
.
Generalized Pareto distributions
There is a hierarchy [1][3] of Pareto distributions known as Pareto Type I, II, III, IV, and Feller–Pareto distributions.[1][3][4] Pareto Type IV contains Pareto Type I–III as special cases. The Feller–Pareto[3][5] distribution generalizes Pareto Type IV.
Pareto types I–IV
The Pareto distribution hierarchy is summarized in the next table comparing the survival functions (complementary CDF).
When μ = 0, the Pareto distribution Type II is also known as the Lomax distribution.[6]
In this section, the symbol xm, used before to indicate the minimum value of x, is replaced by σ.
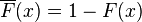 | Support | Parameters | |
|---|---|---|---|
| Type I | ![\left[\frac{x}{\sigma}\right]^{-\alpha}](../I/m/754503cb9857561a994e14a2607dc49c.png) |
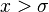 |
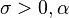 |
| Type II | ![\left[1 + \frac{x-\mu}{\sigma}\right]^{-\alpha}](../I/m/051b4a29e0b5d951d47f6017e42c52f7.png) |
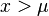 |
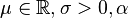 |
| Lomax | ![\left[1 + \frac{x}{\sigma}\right]^{-\alpha}](../I/m/aa0957d9500bf23691b5d0a9588a9d4f.png) |
 |
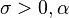 |
| Type III | ![\left[1 + \left(\frac{x-\mu}{\sigma}\right)^{1/\gamma}\right]^{-1}](../I/m/5b4084787066fe93e4a222e1508e6af0.png) |
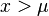 |
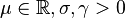 |
| Type IV | ![\left[1 + \left(\frac{x-\mu}{\sigma}\right)^{1/\gamma}\right]^{-\alpha}](../I/m/96bd5217cdaa6b2c2aa325977828a2f6.png) |
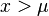 |
 |
The shape parameter α is the tail index, μ is location, σ is scale, γ is an inequality parameter. Some special cases of Pareto Type (IV) are
The finiteness of the mean, and the existence and the finiteness of the variance depend on the tail index α (inequality index γ). In particular, fractional δ-moments are finite for some δ > 0, as shown in the table below, where δ is not necessarily an integer.
![E[X]](../I/m/f564e7c6618bc2c0c99eae5a9376fbaf.png) | Condition | ![E[X^\delta]](../I/m/d19254d3baa31c5180b9638f0861fb8c.png) | Condition | |
|---|---|---|---|---|
| Type I | 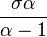 |
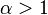 |
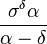 |
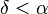 |
| Type II | 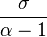 |
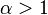 |
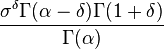 |
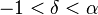 |
| Type III | 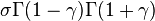 |
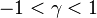 |
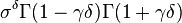 |
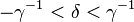 |
| Type IV | 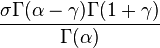 |
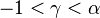 |
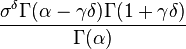 |
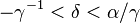 |
Feller–Pareto distribution
Feller[3][5] defines a Pareto variable by transformation U = Y−1 − 1 of a beta random variable Y, whose probability density function is
where B( ) is the beta function. If
then W has a Feller–Pareto distribution FP(μ, σ, γ, γ1, γ2).[1]
If 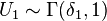 and
and 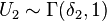 are independent Gamma variables, another construction of a Feller–Pareto (FP) variable is[7]
are independent Gamma variables, another construction of a Feller–Pareto (FP) variable is[7]
and we write W ~ FP(μ, σ, γ, δ1, δ2). Special cases of the Feller–Pareto distribution are
Applications
Pareto originally used this distribution to describe the allocation of wealth among individuals since it seemed to show rather well the way that a larger portion of the wealth of any society is owned by a smaller percentage of the people in that society. He also used it to describe distribution of income.[8] This idea is sometimes expressed more simply as the Pareto principle or the "80-20 rule" which says that 20% of the population controls 80% of the wealth.[9] However, the 80-20 rule corresponds to a particular value of α, and in fact, Pareto's data on British income taxes in his Cours d'économie politique indicates that about 30% of the population had about 70% of the income. The probability density function (PDF) graph at the beginning of this article shows that the "probability" or fraction of the population that owns a small amount of wealth per person is rather high, and then decreases steadily as wealth increases. (Note that the Pareto distribution is not realistic for wealth for the lower end. In fact, net worth may even be negative.) This distribution is not limited to describing wealth or income, but to many situations in which an equilibrium is found in the distribution of the "small" to the "large". The following examples are sometimes seen as approximately Pareto-distributed:
- The sizes of human settlements (few cities, many hamlets/villages)[10]
- File size distribution of Internet traffic which uses the TCP protocol (many smaller files, few larger ones)[10]
- Hard disk drive error rates[11]
- Clusters of Bose–Einstein condensate near absolute zero[12]
- The values of oil reserves in oil fields (a few large fields, many small fields)[10]
- The length distribution in jobs assigned supercomputers (a few large ones, many small ones)
- The standardized price returns on individual stocks [10]
- Sizes of sand particles [10]
- Sizes of meteorites
- Numbers of species per genus (There is subjectivity involved: The tendency to divide a genus into two or more increases with the number of species in it)
- Areas burnt in forest fires
- Severity of large casualty losses for certain lines of business such as general liability, commercial auto, and workers compensation.[13][14]
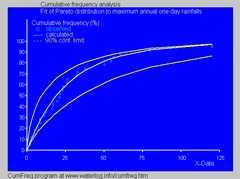
- In hydrology the Pareto distribution is applied to extreme events such as annually maximum one-day rainfalls and river discharges. The blue picture illustrates an example of fitting the Pareto distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.
Relation to other distributions
Relation to the exponential distribution
The Pareto distribution is related to the exponential distribution as follows. If X is Pareto-distributed with minimum xm and index α, then
is exponentially distributed with rate parameter α. Equivalently, if Y is exponentially distributed with rate α, then
is Pareto-distributed with minimum xm and index α.
This can be shown using the standard change of variable techniques:
The last expression is the cumulative distribution function of an exponential distribution with rate α.
Relation to the log-normal distribution
Note that the Pareto distribution and log-normal distribution are alternative distributions for describing the same types of quantities. One of the connections between the two is that they are both the distributions of the exponential of random variables distributed according to other common distributions, respectively the exponential distribution and normal distribution.
Relation to the generalized Pareto distribution
The Pareto distribution is a special case of the generalized Pareto distribution, which is a family of distributions of similar form, but containing an extra parameter in such a way that the support of the distribution is either bounded below (at a variable point), or bounded both above and below (where both are variable), with the Lomax distribution as a special case. This family also contains both the unshifted and shifted exponential distributions.
The Pareto distribution with scale 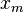 and shape
and shape  is equivalent to the generalized Pareto distribution with location
is equivalent to the generalized Pareto distribution with location 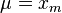 , scale
, scale 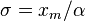 and shape
and shape 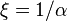 . Vice versa one can get the Pareto distribution from the GPD by
. Vice versa one can get the Pareto distribution from the GPD by 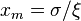 and
and 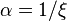 .
.
Relation to Zipf's law
Pareto distributions are continuous probability distributions. Zipf's law, also sometimes called the zeta distribution, may be thought of as a discrete counterpart of the Pareto distribution.
Relation to the "Pareto principle"
The "80-20 law", according to which 20% of all people receive 80% of all income, and 20% of the most affluent 20% receive 80% of that 80%, and so on, holds precisely when the Pareto index is α = log4(5) = log(5)/log(4), approximately 1.161. This result can be derived from the Lorenz curve formula given below. Moreover, the following have been shown[15] to be mathematically equivalent:
- Income is distributed according to a Pareto distribution with index α > 1.
- There is some number 0 ≤ p ≤ 1/2 such that 100p % of all people receive 100(1 − p) % of all income, and similarly for every real (not necessarily integer) n > 0, 100pn % of all people receive 100(1 − p)n percentage of all income.
This does not apply only to income, but also to wealth, or to anything else that can be modeled by this distribution.
This excludes Pareto distributions in which 0 < α ≤ 1, which, as noted above, have infinite expected value, and so cannot reasonably model income distribution.
Lorenz curve and Gini coefficient

The Lorenz curve is often used to characterize income and wealth distributions. For any distribution, the Lorenz curve L(F) is written in terms of the PDF f or the CDF F as
where x(F) is the inverse of the CDF. For the Pareto distribution,
and the Lorenz curve is calculated to be
Although the numerator and denominator in the expression for 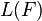 diverge for
diverge for 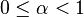 , their ratio does not, yielding L=0 in these cases, which yields a Gini coefficient of unity. Examples of the Lorenz curve for a number of Pareto distributions are shown in the graph on the right.
, their ratio does not, yielding L=0 in these cases, which yields a Gini coefficient of unity. Examples of the Lorenz curve for a number of Pareto distributions are shown in the graph on the right.
The Gini coefficient is a measure of the deviation of the Lorenz curve from the equidistribution line which is a line connecting [0, 0] and [1, 1], which is shown in black (α = ∞) in the Lorenz plot on the right. Specifically, the Gini coefficient is twice the area between the Lorenz curve and the equidistribution line. The Gini coefficient for the Pareto distribution is then calculated (for 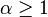 ) to be
) to be
(see Aaberge 2005).
Parameter estimation
The likelihood function for the Pareto distribution parameters α and xm, given a sample x = (x1, x2, ..., xn), is
Therefore, the logarithmic likelihood function is
It can be seen that 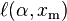 is monotonically increasing with xm, that is, the greater the value of xm, the greater the value of the likelihood function. Hence, since x ≥ xm, we conclude that
is monotonically increasing with xm, that is, the greater the value of xm, the greater the value of the likelihood function. Hence, since x ≥ xm, we conclude that
To find the estimator for α, we compute the corresponding partial derivative and determine where it is zero:
Thus the maximum likelihood estimator for α is:
The expected statistical error is:[16]
Malik (1970)[17] gives the exact joint distribution of 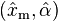 . In particular,
. In particular, 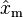 and
and 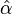 are independent and
are independent and 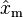 is Pareto with scale parameter xm and shape parameter nα, whereas
is Pareto with scale parameter xm and shape parameter nα, whereas 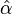 has an Inverse-gamma distribution with shape and scale parameters n−1 and nα, respectively.
has an Inverse-gamma distribution with shape and scale parameters n−1 and nα, respectively.
Graphical representation
The characteristic curved 'Long Tail' distribution when plotted on a linear scale, masks the underlying simplicity of the function when plotted on a log-log graph, which then takes the form of a straight line with negative gradient: It follows from the formula for the probability density function that for x ≥ xm,
Since α is positive, the gradient −(α+1) is negative.
Random sample generation
Random samples can be generated using inverse transform sampling. Given a random variate U drawn from the uniform distribution on the unit interval (0, 1], the variate T given by
is Pareto-distributed.[18] If U is uniformly distributed on [0, 1), it can be exchanged with (1 − U).
Variants
Bounded Pareto distribution
| Parameters |
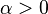 shape (real) shape (real) |
|---|---|
| Support |
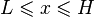 |
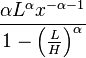 | |
| CDF |
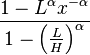 |
| Mean |
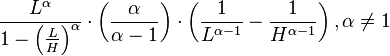 |
| Median |
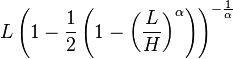 |
| Variance |
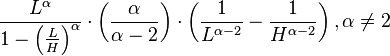 (this is the second moment, NOT the variance) (this is the second moment, NOT the variance) |
| Skewness |
|
The bounded (or truncated) Pareto distribution has three parameters α, L and H. As in the standard Pareto distribution α determines the shape. L denotes the minimal value, and H denotes the maximal value. (The variance in the table on the right should be interpreted as the second moment).
The probability density function is
where L ≤ x ≤ H, and α > 0.
Generating bounded Pareto random variables
If U is uniformly distributed on (0, 1), then applying inverse-transform method [19]
is a bounded Pareto-distributed.
Symmetric Pareto distribution
The symmetric Pareto distribution can be defined by the probability density function:[20]
It has a similar shape to a Pareto distribution for x > xm and is mirror symmetric about the vertical axis.
See also
- Bradford's law
- Pareto analysis
- Pareto efficiency
- Pareto interpolation
- Power law probability distributions
- Traffic generation model
Notes
- ↑ 1.0 1.1 1.2 1.3 Barry C. Arnold (1983). Pareto Distributions. International Co-operative Publishing House. ISBN 0-89974-012-X.
- ↑ 2.0 2.1 Johnson NL, Kotz S, Balakrishnan N (1994) Continuous univariate distributions Vol 1. Wiley Series in Probability and Statistics.
- ↑ 3.0 3.1 3.2 3.3 Johnson, Kotz, and Balakrishnan (1994), (20.4).
- ↑ Christian Kleiber and Samuel Kotz (2003). Statistical Size Distributions in Economics and Actuarial Sciences. Wiley. ISBN 0-471-15064-9.
- ↑ 5.0 5.1 Feller, W. (1971). An Introduction to Probability Theory and its Applications II (2nd ed.). New York: Wiley. p. 50. "The densities (4.3) are sometimes called after the economist Pareto. It was thought (rather naïvely from a modern statistical standpoint) that income distributions should have a tail with a density ~ Ax−α as x → ∞."
- ↑ Lomax, K. S. (1954). Business failures. Another example of the analysis of failure data.Journal of the American Statistical Association, 49, 847–852.
- ↑ Chotikapanich, Duangkamon. "Chapter 7: Pareto and Generalized Pareto Distributions". Modeling Income Distributions and Lorenz Curves. pp. 121–122.
- ↑ Pareto, Vilfredo, Cours d'Économie Politique: Nouvelle édition par G.-H. Bousquet et G. Busino, Librairie Droz, Geneva, 1964, pages 299–345.
- ↑ For a two-quantile population, where approximately 18% of the population owns 82% of the wealth, the Theil index takes the value 1.
- ↑ 10.0 10.1 10.2 10.3 10.4 Reed, William J. et al. (2004.). "The Double Pareto-Lognormal Distribution – A New Parametric Model for Size Distributions". Communications in Statistics – Theory and Methods 33 (8): 1733–1753. doi:10.1081/sta-120037438. CiteSeerX: 10
.1 . Check date values in:.1 .70 .4555 |date=(help) - ↑ Schroeder, Bianca; Damouras, Sotirios; Gill, Phillipa (2010-02-24). "Understanding latent sector error and how to protect against them" (PDF). 8th Usenix Conference on File and Storage Technologies (FAST 2010). Retrieved 2010-09-10.
We experimented with 5 different distributions (Geometric,Weibull, Rayleigh, Pareto, and Lognormal), that are commonly used in the context of system reliability, and evaluated their fit through the total squared differences between the actual and hypothesized frequencies (χ2 statistic). We found consistently across all models that the geometric distribution is a poor fit, while the Pareto distribution provides the best fit.
- ↑ Yuji Ijiri; Simon, Herbert A. (May 1975). "Some Distributions Associated with Bose–Einstein Statistics". Proc. Nat. Acad. Sci. USA 72 (5): 1654–1657. PMC 432601. PMID 16578724. Retrieved 24 January 2013.
- ↑ Kleiber and Kotz (2003): page 94.
- ↑ Seal, H. (1980). "Survival probabilities based on Pareto claim distributions". ASTIN Bulletin 11: 61–71.
- ↑ Hardy, Michael (2010). "Pareto's Law". Mathematical Intelligencer 32 (3): 38–43. doi:10.1007/s00283-010-9159-2.
- ↑ M. E. J. Newman (2005). "Power laws, Pareto distributions and Zipf's law". Contemporary Physics 46 (5): 323–351. arXiv:cond-mat/0412004. Bibcode:2005ConPh..46..323N. doi:10.1080/00107510500052444.
- ↑ H. J. Malik (1970). "Estimation of the Parameters of the Pareto Distribution". Metrika 15.
- ↑ Tanizaki, Hisashi (2004). Computational Methods in Statistics and Econometrics. CRC Press. p. 133.
- ↑ http://www.cs.bgu.ac.il/~mps042/invtransnote.htm
- ↑ Grabchak, M. & Samorodnitsky, D. "Do Financial Returns Have Finite or Infinite Variance? A Paradox and an Explanation" (PDF). pp. 7–8.
References
- M. O. Lorenz (1905). "Methods of measuring the concentration of wealth". Publications of the American Statistical Association 9 (70): 209–219. Bibcode:1905PAmSA...9..209L. doi:10.2307/2276207.
- Pareto V (1965) "La Courbe de la Repartition de la Richesse" (Originally published in 1896). In: Busino G, editor. Oevres Completes de Vilfredo Pareto. Geneva: Librairie Droz. pp. 1–5.
- Pareto, V. (1895). La legge della domanda. Giornale degli Economisti, 10, 59–68. English translation in Rivista di Politica Economica, 87 (1997), 691–700.
- Pareto, V. (1897). Cours d'économie politique. Lausanne: Ed. Rouge.
External links
- Gini's Nuclear Family / Rolf Aabergé. – In: International Conference to Honor Two Eminent Social Scientists, May, 2005 – PDF
- Hazewinkel, Michiel, ed. (2001), "Pareto distribution", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- syntraf1.c is a C program to generate synthetic packet traffic with bounded Pareto burst size and exponential interburst time.
- "Self-Similarity in World Wide Web Traffic: Evidence and Possible Causes" /Mark E. Crovella and Azer Bestavros
- Weisstein, Eric W., "Pareto distribution", MathWorld.
| ||||||||||||||

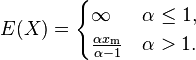
![\mathrm{Var}(X)= \begin{cases}
\infty & \alpha\in(1,2], \\
\left(\frac{x_\mathrm{m}}{\alpha-1}\right)^2 \frac{\alpha}{\alpha-2} & \alpha>2.
\end{cases}](../I/m/eca4aebe665f42fd089a6a487e2f4e4e.png)
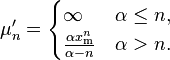
![M\left(t;\alpha,x_\mathrm{m}\right) = E \left [e^{tX} \right ] = \alpha(-x_\mathrm{m} t)^\alpha\Gamma(-\alpha,-x_\mathrm{m} t)](../I/m/32bd805327fa6064a335d3c4ef472a63.png)