Parametric model
In statistics, a parametric model or parametric family or finite-dimensional model is a family of distributions that can be described using a finite number of parameters. These parameters are usually collected together to form a single k-dimensional parameter vector θ = (θ1, θ2, …, θk).
Parametric models are contrasted with the semi-parametric, semi-nonparametric, and non-parametric models, all of which consist of an infinite set of “parameters” for description. The distinction between these four classes is as follows:
- in a “parametric” model all the parameters are in finite-dimensional parameter spaces;
- a model is “non-parametric” if all the parameters are in infinite-dimensional parameter spaces;
- a “semi-parametric” model contains finite-dimensional parameters of interest and infinite-dimensional nuisance parameters;
- a “semi-nonparametric” model has both finite-dimensional and infinite-dimensional unknown parameters of interest.
Some statisticians believe that the concepts “parametric”, “non-parametric”, and “semi-parametric” are ambiguous.[1] It can also be noted that the set of all probability measures has cardinality of continuum, and therefore it is possible to parametrize any model at all by a single number in (0,1) interval.[2] This difficulty can be avoided by considering only “smooth” parametric models.
Definition
A parametric model is a collection of probability distributions such that each member of this collection, Pθ, is described by a finite-dimensional parameter θ. The set of all allowable values for the parameter is denoted Θ ⊆ Rk, and the model itself is written as
When the model consists of absolutely continuous distributions, it is often specified in terms of corresponding probability density functions:
The parametric model is called identifiable if the mapping θ ↦ Pθ is invertible, that is there are no two different parameter values θ1 and θ2 such that Pθ1 = Pθ2.
Examples
- The Poisson family of distributions is parametrized by a single number λ > 0:
where pλ is the probability mass function. This family is an exponential family.
-
- The normal family is parametrized by θ = (μ,σ), where μ ∈ R is a location parameter, and σ > 0 is a scale parameter. This parametrized family is both an exponential family and a location-scale family:
-
- The Weibull translation model has three parameters θ = (λ, β, μ):
This model is not regular (see definition below) unless we restrict β to lie in the interval (2, +∞).
-
Regular parametric model
Let μ be a fixed σ-finite measure on a probability space (Ω, ℱ), and  the collection of all probability measures dominated by μ. Then we will call
the collection of all probability measures dominated by μ. Then we will call  a regular parametric model if the following requirements are met:[3]
a regular parametric model if the following requirements are met:[3]
- Θ is an open subset of Rk.
- The map
from Θ to L2(μ) is Fréchet differentiable: there exists a vector
 such that
such thatwhere ′ denotes matrix transpose.
-
- The map
 (defined above) is continuous on Θ.
(defined above) is continuous on Θ. - The k×k Fisher information matrix
is non-singular.
-
Properties
- Sufficient conditions for regularity of a parametric model in terms of ordinary differentiability of the density function ƒθ are following:[4]
- The density function ƒθ(x) is continuously differentiable in θ for μ-almost all x, with gradient ∇ƒθ.
- The score function
belongs to the space L²(Pθ) of square-integrable functions with respect to the measure Pθ.
-
- The Fisher information matrix I(θ), defined as
is nonsingular and continuous in θ.
-
If conditions (i)−(iii) hold then the parametric model is regular.
- Local asymptotic normality.
- If the regular parametric model is identifiable then there exists a uniformly
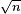 -consistent and efficient estimator of its parameter θ.[5]
-consistent and efficient estimator of its parameter θ.[5]
See also
- Statistical model
- Parametric family
- Parametrization (i.e., coordinate system)
- Parsimony (with regards to the trade-off of many or few parameters in data fitting)
- Parametricism
Notes
- ↑ LeCam 2000, ch.7.4
- ↑ Bickel 1998, p. 2
- ↑ Bickel 1998, p. 12
- ↑ Bickel 1998, p.13, prop.2.1.1
- ↑ Bickel 1998, Theorems 2.5.1, 2.5.2
References
- Bickel, Peter J. and Doksum, Kjell A. (2001). Mathematical Statistics: Basic and Selected Topics, Volume 1. (Second (updated printing 2007) ed.). Pearson Prentice-Hall.
- Bickel, Peter J.; Klaassen, Chris A.J.; Ritov, Ya’acov; Wellner Jon A. (1998). Efficient and adaptive estimation for semiparametric models. Springer: New York. ISBN 0-387-98473-9.
- Davidson, A.C. (2003). Statistical Models. Cambridge University Press.
- Freedman, David A. (2009). Statistical Models: Theory and Practice (Second ed.). Cambridge University Press. ISBN 978-0-521-67105-7.
- Le Cam, Lucien; Lo Yang, Grace (2000). Asymptotics in statistics: some basic concepts. Springer. ISBN 0-387-95036-2.
- Lehmann, Erich (1983). Theory of Point Estimation.
- Lehmann, Erich (1959). Testing Statistical Hypotheses.
- Liese, Friedrich and Miescke, Klaus-J. (2008). Statistical Decision Theory: Estimation, Testing, and Selection. Springer.
- Pfanzagl, Johann; with the assistance of R. Hamböker (1994). Parametric Statistical Theory. Walter de Gruyter. ISBN 3-11-013863-8. MR 1291393









