Parallelohedron
In geometry a parallelohedron is a polyhedron that can tessellate 3-dimensional spaces with face-to-face contacts via translations. This requires all opposite faces be congruent. Parallelohedra can only have parallelogonal faces, either parallelograms or hexagons with parallel opposite edges.
There are 5 types, first identified by Evgraf Fedorov in his studies of crystallographic systems.
Topological types
The vertices of parallelohedra can be computed by linear combinations of 3 to 6 vectors. Each vector can have any length greater than zero, with zero length becoming degenerate, or becoming a smaller parallelohedra.
The greatest parallelohedron is a truncated octahedron which is also called a 4-permutahedron and can be represented with in a 4D in a hyperplane coordinates as all permutations of the counting numbers (1,2,3,4).
A belt mn means n directional vectors, each containing m coparallel congruent edges. Every type has order 2 Ci central inversion symmetry in general, but each has higher symmetry geometries as well.
| Name | Cube (parallelepiped) |
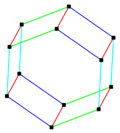
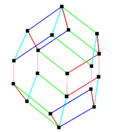
Rhombic dodecahedron | Hexagonal prism Elongated cube |
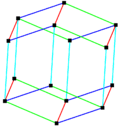
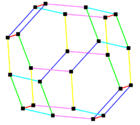
Elongated dodecahedron | Truncated octahedron |
|---|---|---|---|---|---|
| Images |  |
 |
 |
 |
 |
| Edge types |
3 edge-lengths | 4 edge-lengths | 3+1 edge-lengths | 4+1 edge-lengths | 6 edge-lengths |
| Belts | 43 | 64 | 43, 61 | 64, 41 | 66 |
Symmetries of 5 types
There are 5 types of parallelohedra, although each has forms of varied symmetry.
| # | Polyhedron | Symmetry (order) | Image | Vertices | Edges | Faces | Belts |
|---|---|---|---|---|---|---|---|
| 1 | Rhombohedron | Ci (2) | 8 | 12 | 6 | 43 | |
| Trigonal trapezohedron | D3d (12) | ||||||
| Parallelepiped | Ci (2) | ||||||
| Rectangular cuboid | D2h (8) | ||||||
| Cube | Oh (24) | ||||||
| 2 | Hexagonal prism | Ci (2) | 8 | 18 | 12 | 61, 43 | |
| D6h (24) |  | ||||||
| 3 | Rhombic dodecahedron | D2h (8) | 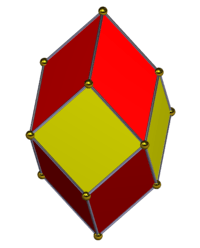 |
14 | 24 | 12 | 64 |
| Oh (24) |  | ||||||
| 4 | Elongated dodecahedron | D4h (16) |  | 18 | 28 | 12 | 64, 41 |
| D2h (8) | |||||||
| 5 | Truncated octahedron | Oh (24) | 24 | 36 | 14 | 66 |
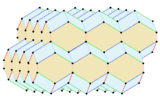
Examples
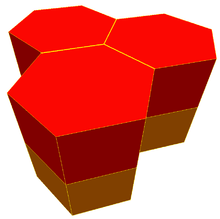
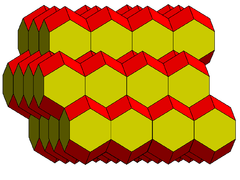
| Pm3m (221) | Im3m (229) | Fm3m (225) | ||
|---|---|---|---|---|
 |
 |
 |
 |
 |
| Cubic |
Hexagonal prismatic |
Rhombic dodecahedral |
Elongated dodecahedral | Bitruncated cubic |
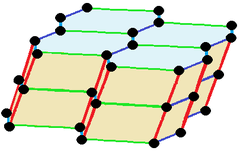
| General symmetry examples | ||||
 |
 |
 |
||
See also
- parallelogon - analogous space-filling polygons in 2D, with parallelograms and hexagons
- parallelotope
References
- The facts on file: Geometry handbook, Catherine A. Gorini, 2003, ISBN 0-8160-4875-4, p.117
- Coxeter, H. S. M. Regular polytopes (book), 3rd ed. New York: Dover, pp. 29-30, p.257, 1973.
- Tutton, A. E. H. Crystallography and Practical Crystal Measurement, 2nd ed. London: Lubrecht & Cramer, 1964.
- Weisstein, Eric W., "Primary parallelohedron", MathWorld.
- Weisstein, Eric W., "Space-filling polyhedron", MathWorld.
- E. S. Fedorov, Nachala Ucheniya o Figurah. [In Russian] (Elements of the theory of figures) Notices Imper. Petersburg Mineralog. Soc., 2nd ser.,24(1885), 1 – 279. Republished by the Acad. Sci. USSR, Moscow 1953.
- Fedorov's five parallelohedra in R³
- Fedorov's Five Parallelohedra