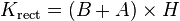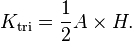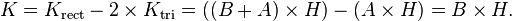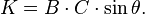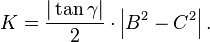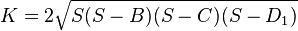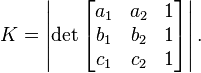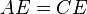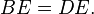Parallelogram

This article is about the quadrilateral shape. For the album by Linda Perhacs, see Parallelograms (album).

Parallelogram
This parallelogram is a rhomboid as it has no right angles and unequal sides.
Type	quadrilateral
Edges and vertices	4
Symmetry group	C₂, [2]⁺, (22)
Area	b × h (base × height); ab sin θ (product of adjacent sides and sine of any vertex angle)
Properties	convex

In Euclidean geometry, a parallelogram is a (non self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean Parallel Postulate and neither condition can be proven without appealing to the Euclidean Parallel Postulate or one of its equivalent formulations. The three-dimensional counterpart of a parallelogram is a parallelepiped. A quadrilateral with one pair of parallel sides is a trapezoid in American English or a trapezium in British English.

The etymology (in Greek παραλληλ-όγραμμον, a shape "of parallel lines") reflects the definition.

Special cases

Quadrilaterals by symmetry

Rhomboid – A quadrilateral whose opposite sides are parallel and adjacent sides are unequal, and whose angles are not right angles^[1]
Rectangle – A parallelogram with four angles of equal size
Rhombus – A parallelogram with four sides of equal length.
Square – A parallelogram with four sides of equal length and angles of equal size (right angles).

Characterizations

A simple (non self-intersecting) quadrilateral is a parallelogram if and only if any one of the following statements is true:^[2]^[3]

Two pairs of opposite sides are equal in length.
Two pairs of opposite angles are equal in measure.
The diagonals bisect each other.
One pair of opposite sides are parallel and equal in length.
Adjacent angles are supplementary.
Each diagonal divides the quadrilateral into two congruent triangles.
The sum of the squares of the sides equals the sum of the squares of the diagonals. (This is the parallelogram law.)
It has rotational symmetry of order 2.

Properties

Diagonals of a parallelogram bisect each other,
Opposite sides of a parallelogram are parallel (by definition) and so will never intersect.
The area of a parallelogram is twice the area of a triangle created by one of its diagonals.
The area of a parallelogram is also equal to the magnitude of the vector cross product of two adjacent sides.
Any line through the midpoint of a parallelogram bisects the area.^[4]
Any non-degenerate affine transformation takes a parallelogram to another parallelogram.
A parallelogram has rotational symmetry of order 2 (through 180°). If it also has two lines of reflectional symmetry then it must be a rhombus or an oblong.
The perimeter of a parallelogram is 2(a + b) where a and b are the lengths of adjacent sides.
The sum of the distances from any interior point of a parallelogram to the sides is independent of the location of the point. (This is an extension of Viviani's theorem). The converse also holds: If the sum of the distances from a point in the interior of a quadrilateral to the sides is independent of the location of the point, then the quadrilateral is a parallelogram.^[5]
Unlike any other convex polygon, a parallelogram cannot be inscribed in any triangle with less than twice its area.^[6]

Area formula

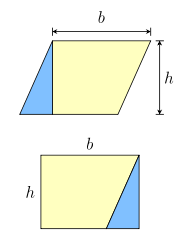
A parallelogram with base b and height h can be divided into a trapezoid and a right triangle, and rearranged into a rectangle, as shown in the figure to the left. This means that the area of a parallelogram is the same as that of a rectangle with the same base and height:

A diagram showing how a parallelogram can be re-arranged into the shape of a rectangle

A parallelogram can be rearranged into a rectangle with the same area.

$K = bh.$

The area of the parallelogram is the area of the blue region, which is the interior of the parallelogram

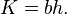
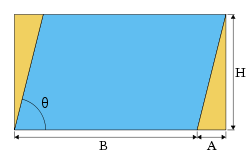
The base × height area formula can also be derived using the figure to the right. The area K of the parallelogram to the right (the blue area) is the total area of the rectangle less the area of the two orange triangles.

The area of the rectangle is

K_\text{rect} = (B+A) \times H\,

and the area of a single orange triangle is

K_\text{tri} = \frac{1}{2} A \times H. \,

Therefore, the area of the parallelogram is

K = K_\text{rect} - 2 \times K_\text{tri} = ( (B+A) \times H) - ( A \times H) = B \times H.

Another area formula, for two sides B and C and angle θ, is

K = B \cdot C \cdot \sin \theta.\,

The area of a parallelogram with sides B and C (B ≠ C) and angle 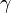$\gamma$ at the intersection of the diagonals is given by^[7]

K = \frac{|\tan \gamma|}{2} \cdot \left| B^2 - C^2 \right|.

When the parallelogram is specified from the lengths B and C of two adjacent sides together with the length D₁ of either diagonal, then the area can be found from Heron's formula. Specifically it is

K=2\sqrt{S(S-B)(S-C)(S-D_1)}

where

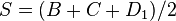S=(B+C+D_1)/2

and the leading factor 2 comes from the fact that the number of congruent triangles that the chosen diagonal divides the parallelogram into is two.

Another parallelogram with the same base and height

Given any parallelogram divided in half through one of the diagonals, one can move one of the triangles to the other side of the other triangle to get another parallelogram with the same base and height, and thus the same area.

Area in terms of Cartesian coordinates of vertices

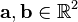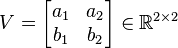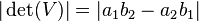Let vectors $\mathbf{a},\mathbf{b}\in\R^2$ and let $V = \begin{bmatrix} a_1 & a_2 \\ b_1 & b_2 \end{bmatrix} \in\R^{2 \times 2}$ denote the matrix with elements of a and b. Then the area of the parallelogram generated by a and b is equal to $|\det(V)| = |a_1b_2 - a_2b_1|\,$ .

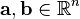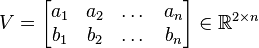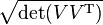Let vectors $\mathbf{a},\mathbf{b}\in\R^n$ and let $V = \begin{bmatrix} a_1 & a_2 & \dots & a_n \\ b_1 & b_2 & \dots & b_n \end{bmatrix} \in\R^{2 \times n}$ . Then the area of the parallelogram generated by a and b is equal to $\sqrt{\det(V V^\mathrm{T})}$ .

Let points 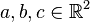$a,b,c\in\R^2$ . Then the area of the parallelogram with vertices at a, b and c is equivalent to the absolute value of the determinant of a matrix built using a, b and c as rows with the last column padded using ones as follows:

K = \left| \det \begin{bmatrix} a_1 & a_2 & 1 \\ b_1 & b_2 & 1 \\ c_1 & c_2 & 1 \end{bmatrix} \right|.

Proof that diagonals bisect each other

To prove that the diagonals of a parallelogram bisect each other, we will use congruent triangles:

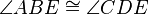\angle ABE \cong \angle CDE

(alternate interior angles are equal in measure)

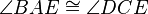\angle BAE \cong \angle DCE

(alternate interior angles are equal in measure).

(since these are angles that a transversal makes with parallel lines AB and DC).

Also, side AB is equal in length to side DC, since opposite sides of a parallelogram are equal in length.

Therefore triangles ABE and CDE are congruent (ASA postulate, two corresponding angles and the included side).

Therefore,

AE = CE

BE = DE.

Since the diagonals AC and BD divide each other into segments of equal length, the diagonals bisect each other.

Separately, since the diagonals AC and BD bisect each other at point E, point E is the midpoint of each diagonal.

Parallelograms arising from other figures

Automedian triangle

An automedian triangle is one whose medians are in the same proportions as its sides (though in a different order). If ABC is an automedian triangle in which vertex A stands opposite the side a, G is the centroid (where the three medians of ABC intersect), and AL is one of the extended medians of ABC with L lying on the circumcircle of ABC, then BGCL is a parallelogram.

Varignon parallelogram

The midpoints of the sides of an arbitrary quadrilateral are the vertices of a parallelogram, called its Varignon parallelogram. If the quadrilateral is convex or concave (that is, not self-intersecting), then the area of the Varignon parallelogram is half the area of the quadrilateral.

Tangent parallelogram of an ellipse

For an ellipse, two diameters are said to be conjugate if and only if the tangent line to the ellipse at an endpoint of one diameter is parallel to the other diameter. Each pair of conjugate diameters of an ellipse has a corresponding tangent parallelogram, sometimes called a bounding parallelogram, formed by the tangent lines to the ellipse at the four endpoints of the conjugate diameters. All tangent parallelograms for a given ellipse have the same area.

It is possible to reconstruct an ellipse from any pair of conjugate diameters, or from any tangent parallelogram.

Faces of a parallelepiped

A parallelepiped is a three-dimensional figure whose six faces are parallelograms.

References

↑ http://www.cimt.plymouth.ac.uk/resources/topics/art002.pdf
↑ Owen Byer, Felix Lazebnik and Deirdre Smeltzer, Methods for Euclidean Geometry, Mathematical Association of America, 2010, pp. 51-52.
↑ Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition", Information Age Publishing, 2008, p. 22.
↑ Dunn, J.A., and J.E. Pretty, "Halving a triangle", Mathematical Gazette 56, May 1972, p. 105.
↑ Chen, Zhibo, and Liang, Tian. "The converse of Viviani's theorem", The College Mathematics Journal 37(5), 2006, pp. 390–391.
↑ Weisstein, Eric W. "Triangle Circumscribing". Wolfram Math World.
↑ Mitchell, Douglas W., "The area of a quadrilateral", Mathematical Gazette, July 2009.

External links

Wikimedia Commons has media related to Parallelograms.

Parallelogram and Rhombus - Animated course (Construction, Circumference, Area)
Weisstein, Eric W., "Parallelogram", MathWorld.
Interactive Parallelogram --sides, angles and slope
Area of Parallelogram at cut-the-knot
Equilateral Triangles On Sides of a Parallelogram at cut-the-knot
Definition and properties of a parallelogram with animated applet
Interactive applet showing parallelogram area calculation interactive applet