Parallelization (mathematics)
In mathematics, a parallelization[1] of a manifold 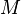 of dimension n is a set of n global linearly independent vector fields.
of dimension n is a set of n global linearly independent vector fields.
Formal definition
Given a manifold 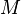 of dimension n, a parallelization of
of dimension n, a parallelization of 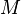 is a set
is a set 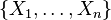 of n vector fields defined on all of
of n vector fields defined on all of 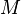 such that for every
such that for every 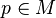 the set
the set 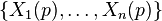 is a basis of
is a basis of 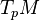 , where
, where 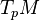 denotes the fiber over
denotes the fiber over 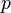 of the tangent vector bundle
of the tangent vector bundle 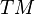 .
.
A manifold is called parallelizable whenever admits a parallelization.
Examples
- Every Lie group is a parallelizable manifold.
- The product of parallelizable manifolds is parallelizable.
- Every affine space, considered as manifold, is parallelizable.
Properties
Proposition. A manifold 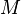 is parallelizable iff there is a diffeomorphism
is parallelizable iff there is a diffeomorphism 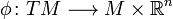 such that the first projection of
such that the first projection of 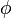 is
is 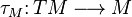 and for each
and for each 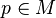 the second factor—restricted to
the second factor—restricted to 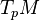 —is a linear map
—is a linear map 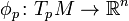 .
.
In other words, 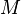 is parallelizable if and only if
is parallelizable if and only if 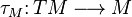 is a trivial bundle. For example suppose that
is a trivial bundle. For example suppose that 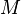 is an open subset of
is an open subset of 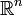 , i.e., an open submanifold of
, i.e., an open submanifold of 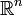 . Then
. Then 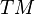 is equal to
is equal to 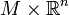 , and
, and 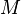 is clearly parallelizable.[2]
is clearly parallelizable.[2]
See also
- Chart (topology)
- Differentiable manifold
- Frame bundle
- Orthonormal frame bundle
- Principal bundle
- Connection (mathematics)
- G-structure
- Web (differential geometry)
Notes
- ↑ Bishop & Goldberg (1968), p. 160
- ↑ Milnor & Stasheff (1974), p. 15.
References
- Bishop, R.L.; Goldberg, S.I. (1968), Tensor Analysis on Manifolds (First Dover 1980 ed.), The Macmillan Company, ISBN 0-486-64039-6
- Milnor, J.W.; Stasheff, J.D. (1974), Characteristic Classes, Princeton University Press